题目内容
20.已知直线y=$\frac{1}{3}x+\frac{2}{3}$与幂函数f(x)=xm(m≠0)的图象将于A、B两点,且|AB|=$\sqrt{10}$,则m的值为( )| A. | -2 | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
分析 分别取幂函数的指数为四个选项,然后判断交点情况,若有两个交点,求出直线被曲线所截线段长,则答案可求.
解答 解:若m=-2,联立$\left\{\begin{array}{l}{y=\frac{1}{3}x+\frac{2}{3}}\\{y={x}^{-2}}\end{array}\right.$,得(x-1)(x2+3x+3)=0,即x=1.
说明m=-2时,直线y=$\frac{1}{3}x+\frac{2}{3}$与幂函数f(x)=xm(m≠0)的图象只有一个交点,不合题意;
由幂函数的图象可知,m=-$\frac{1}{2}$时,直线y=$\frac{1}{3}x+\frac{2}{3}$与幂函数f(x)=xm(m≠0)的图象只有一个交点,不合题意;
当m=$\frac{1}{2}$时,联立$\left\{\begin{array}{l}{y=\frac{1}{3}x+\frac{2}{3}}\\{y={x}^{\frac{1}{2}}}\end{array}\right.$,得$x-3\sqrt{x}+2=0$,解得x1=1,x2=4.
当x1=1时,y1=1;当x2=4时,y2=2.
∴A(1,1),B(4,2).
则$|AB|=\sqrt{(4-1)^{2}+(2-1)^{2}}=\sqrt{10}$,符合题意;
当m=2时,联立$\left\{\begin{array}{l}{y=\frac{1}{3}x+\frac{2}{3}}\\{y={x}^{2}}\end{array}\right.$,解得A($-\frac{2}{3},\frac{4}{9}$),B(1,1),
|AB|=$\sqrt{(1+\frac{2}{3})^{2}+(1-\frac{4}{9})^{2}}=\frac{5\sqrt{2}}{3}$,不合题意.
故选:C.
点评 本题考查了命题的真假判断与应用,考查了直线和曲线的交点问题,是中档题.

| A. | x2-$\frac{y^2}{4}$=1 | B. | $\frac{x^2}{4}$-y2=1 | C. | x2-$\frac{y^2}{2}$=1 | D. | $\frac{x^2}{2}$-y2=1 |
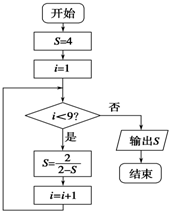
| A. | -1 | B. | $\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | 4 |
| A. | l与l1,l2都不相交 | B. | l与l1,l2都相交 | ||
| C. | l至多与l1,l2中的一条相交 | D. | l至少与l1,l2中的一条相交 |
