题目内容
17．数列{an}中a1=0，a4=-7，当n≥2时，（1-an）2=（1-an+1）（1-an-1），则数列{an}的前n项和为n+1-2n．分析 根据条件得到数列{1-an}为等比数列，求出数列的通项公式，进行求和即可．
解答 解：由（1-an）2=（1-an+1）（1-an-1），
得数列{1-an}为等比数列，
首项为1-a1=1，第四项为1-a4=1+7=8，
设公比q，则1-a4=1×q3=8，
解得q=2，
则1-an=2n-1，
即an=1-2n-1，
则数列{an}的前n项和为Sn=n-$\frac{1-{2}^{n}}{1-2}$=n+1-2n，
故答案为：n+1-2n
点评 本题主要考查数列求和，根据条件判断数列是等比数列是解决本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
如图，在⊙O中，相交于点E的两弦AB，CD的中点分别是M，N，直线MO与直线CD相交于点F，证明：
5．执行如图所示的程序框图，则输出的S值是（ ）
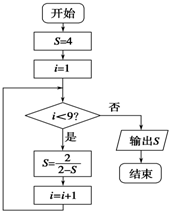
| A． | -1 | B． | $\frac{2}{3}$ | C． | $\frac{3}{2}$ | D． | 4 |
2．给出两个命题：命题p：不等式0＜α＜π成立是不等式sinα＞0成立的必要不充分条件；命题q：函数y=log2（$\sqrt{{x}^{2}+1}$-x）是奇函数，则下列命题是真命题的是（ ）
| A． | p∧q | B． | p∨￢q | C． | p∨q | D． | p∧￢q |
6．已知等腰直角三角形的直角边的长为2，将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积为（ ）
| A． | $\frac{2\sqrt{2}π}{3}$ | B． | $\frac{4\sqrt{2}π}{3}$ | C． | 2$\sqrt{2}$π | D． | 4$\sqrt{2}$π |