题目内容
10.若点P是椭圆$\frac{{x}^{2}}{2}$+y2=1上的动点,则P到直线l:y=x+1的距离的最大值是$\frac{\sqrt{2}+\sqrt{6}}{2}$.分析 设出P的坐标,利用点到直线的距离公式,结合辅助角公式,即可求出到直线l:y=x+1的距离的最大值.
解答 解:设P($\sqrt{2}$cosθ,sinθ),则
P到直线l:y=x+1的距离d=$\frac{|\sqrt{2}cosθ-sinθ+1|}{\sqrt{2}}$=$\frac{|\sqrt{3}sin(θ+α)+1|}{\sqrt{2}}$,
∴P到直线l:y=x+1的距离的最大值是$\frac{\sqrt{3}+1}{\sqrt{2}}$=$\frac{\sqrt{2}+\sqrt{6}}{2}$.
故答案为:$\frac{\sqrt{2}+\sqrt{6}}{2}$.
点评 本题考查椭圆的参数方程,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
20. 在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C为正态分布N(0,1)的密度曲线)的点的个数的估计值为( )
在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C为正态分布N(0,1)的密度曲线)的点的个数的估计值为( )
附“若X-N=(μ,a2),则
P(μ-σ<X≤μ+σ)=0.6826.
p(μ-2σ<X≤μ+2σ)=0.9544.
 在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C为正态分布N(0,1)的密度曲线)的点的个数的估计值为( )
在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C为正态分布N(0,1)的密度曲线)的点的个数的估计值为( )附“若X-N=(μ,a2),则
P(μ-σ<X≤μ+σ)=0.6826.
p(μ-2σ<X≤μ+2σ)=0.9544.
| A. | 2386 | B. | 2718 | C. | 3413 | D. | 4772 |
1.随着三星S6手机的上市,很多消费者觉得价格偏高,尤其是大部分学生可望而不可及,因此我市沃尔玛“三星手机专卖店”推出无抵押分期付款购买方式,该店对最近100名采用分期付款的购买者进行统计,统计结果如下表所示:
已知分3期付款的频率为0.15,并且店销售一部三星S6,顾客分1期付款,其利润为1000元;分2期或3期付款,其利润为1500元;分4期或5期付款,其利润为2000元,以频率作为概率.以此样本估计总体,试解决以下问题
(Ⅰ)求事件A:“购买的3位顾客中,恰好有1名顾客分4期付款”的概率;
(Ⅱ)用X表示销售一部三星S6手机的利润,求X的分布列及数学期望.
| 付款方式 | 分1期 | 分2期 | 分3期 | 分4期 | 分5期 |
| 频 数 | 35 | 25 | a | 10 | b |
(Ⅰ)求事件A:“购买的3位顾客中,恰好有1名顾客分4期付款”的概率;
(Ⅱ)用X表示销售一部三星S6手机的利润,求X的分布列及数学期望.
18.若直线ax+by=4与不等式组$\left\{\begin{array}{l}{2x-5y+8≥0}\\{2x+y-4≤0}\\{x+2y+4≥0}\end{array}\right.$表示的平面区域无公共点,则a+b的取值范围( )
| A. | ($\frac{3}{2}$,3) | B. | (-3,3) | C. | (-3,$\frac{3}{2}$) | D. | (-1,3) |
5.执行如图所示的程序框图,则输出的S值是( )
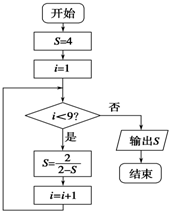

| A. | -1 | B. | $\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | 4 |
2.给出两个命题:命题p:不等式0<α<π成立是不等式sinα>0成立的必要不充分条件;命题q:函数y=log2($\sqrt{{x}^{2}+1}$-x)是奇函数,则下列命题是真命题的是( )
| A. | p∧q | B. | p∨¬q | C. | p∨q | D. | p∧¬q |
20.某校老年、中年和青年教师的人数见如表,采用分层插样的方法调查教师的身体状况,在抽取的样本中,青年教师有320人,则该样本的老年教师人数为( )
| 类别 | 人数 |
| 老年教师 | 900 |
| 中年教师 | 1800 |
| 青年教师 | 1600 |
| 合计 | 4300 |
| A. | 90 | B. | 100 | C. | 180 | D. | 300 |