题目内容
【题目】已知函数![]() 图象上一点
图象上一点![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求![]() 的值;
的值;
(2)若方程![]() 在
在![]() 内有两个不等实根,求
内有两个不等实根,求![]() 的取值范围(其中
的取值范围(其中
![]() 为自然对数的底).
为自然对数的底).
【答案】(1)a=2,b=1.(2) ![]() .
.
【解析】试题分析:
本题考查函数与方程,函数与导数的综合应用.(1)根据导数的几何意义,得出两个方程,然后求解.(2)先利用导数研究函数h(x)=f(x)+m=2lnx﹣x2+m的单调性,根据单调性与极值点确定关系然后求解.
试题解析:
(1)∵![]() ,
,
∴![]()
由题意得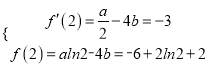 ,
,
解得![]() .
.
(2)由(1)得f(x)=2lnx﹣x2,
令h(x)=f(x)+m=2lnx﹣x2+m,
则![]() ,
,
令h'(x)=0,得x=1(x=﹣1舍去).
故当x∈![]() 时,h'(x)>0,h(x)单调递增;
时,h'(x)>0,h(x)单调递增;
当x∈(1,e]时,h'(x)<0,h(x)单调递减.
∵方程h(x)=0在![]() 内有两个不等实根,
内有两个不等实根,
∴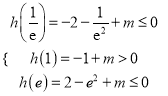 ,解得
,解得![]() .
.
∴实数![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目