题目内容
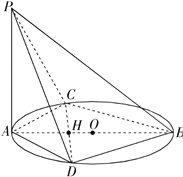
【题目】已知AB是圆O的直径,C,D是圆上不同两点,且CD∩AB=H,AC=AD,PA⊥圆O所在平面.
(Ⅰ)求证:PB⊥CD;
(Ⅱ)若PB=![]() ,∠PBA=
,∠PBA=![]() ,∠CAD=
,∠CAD=![]() ,求H到平面PBD的距离.
,求H到平面PBD的距离.
【答案】(Ⅰ)证明见解析;(Ⅱ) ![]() .
.
【解析】试题分析:(Ⅰ)由AB是圆O的直径知∠ACB=∠ADB=90°,从而证明PB⊥CD.(Ⅱ)过点P作PB的垂线,过点H作PB的垂线,分别交PB于点E,F;求出H到平面PBD的距离.
试题解析:
(Ⅰ)证明:∵AB是圆O的直径,
∴∠ACB=∠ADB=![]() ,
,
∵AC=AD,∴Rt△ACB≌Rt△ADB,∴AB⊥CD,
又∵PA⊥圆O所在平面,CD在圆O所在平面内,
∴PA⊥CD,
∵PA∩AB=A,∴CD⊥平面PAB,∴PB⊥CD.
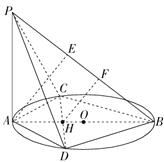
(Ⅱ)解:过点A作PB的垂线,过点H作PB的垂线,分别交PB于E,F,
∵Rt△PAB中,∠PBA=![]() ,PB=2
,PB=2![]() ,
,
∴PA=AB=2,∴AE=ABsin![]() =2·
=2·![]() =
=![]() ,
,
又∵∠CAB=∠DAB=![]() ,∴AC=1,AD=1
,∴AC=1,AD=1
∵CH⊥AH,∴AH=![]() ,
,
∴BH=![]() ,HD=
,HD=![]() ,BD=
,BD=![]() ,PD=
,PD=![]()
∴VH-PBD=VP-HDB=![]() ×
×![]() ×
×![]() ×
×![]() ×2=
×2=![]()
S△PBD=![]() ×
×![]() ×
×![]() =
=![]() ,
,
∴H到平面PBD的距离为![]() =
=![]() .
.

练习册系列答案
相关题目