题目内容
【题目】已知函数
的定义域为
，值域是
.
（Ⅰ）求证: 
；
（Ⅱ）求实数
的取值范围.
【答案】(Ⅰ) 见解析(Ⅱ) 
.
【解析】试题分析：(1)根据已知函数求出定义域，则
为已知函数所求出的x的范围的子集，再利用所提供的值域得出m>1,n>1的要求，从而说明m>3；(2)根据复合函数的单调性法则，由于对数的底数0<a<1,以及
的单调性判断出原函数f(x)在
上为增函数，根据已知定义域和值域及函数的单调性，写出x值与y值的对应关系式，得出列方程组，把问题转化为一元二次方程存在两个大于3的实根问题，最后利用根的分布条件列出不等式组，解出a的范围.
试题解析：
(Ⅰ) 
,又因为函数的定义域
，可得
或
,
而函数的值域为
，由对数函数的性质知
， 
(Ⅱ) 
在区间
上递增,又因为
即
单调递减的函数.
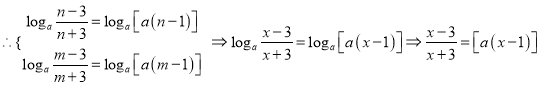
即
有两个大于3的实数根，
.
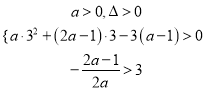
练习册系列答案
相关题目
【题目】已知x与y之间的几组数据如下表：
x | 1 | 2 | 3 | 4 | 5 | 6 |
y | 0 | 2 | 1 | 3 | 3 | 4 |
假设根据上表数据所得的线性回归方程为
＝
x＋
.若某同学根据上表中的前两组数据(1,0)和(2,2)求得的直线方程为y＝b′x＋a′，则以下结论正确的是( )
A. 
>b′，
>a′ B. >b′，<a′
C. <b′，>a′ D. <b′，<a′
