题目内容
【题目】如图,五面体ABCDE,四边形ABDE是矩形,△ABC是正三角形,AB=1,AE=2,F是线段BC上一点,直线BC与平面ABD所成角为30°,CE∥平面ADF.
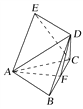
(1)试确定F的位置;
(2)求三棱锥A-CDF的体积.
【答案】(1)F是BC的中点.(2) ![]() .
.
【解析】试题分析:(1)连接BE交AD于点O,取BC的中点F,再根据三角形中位线性质得CE∥OF,最后根据线面平行判定定理得线面平行(2)根据直线BC与平面ABD所成角为30°,可得C到平面ABD的距离,再利用等体积法求三棱锥A-CDF的体积.
试题解析:(1)证明 连接BE交AD于点O,连接OF,
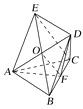
∵CE∥平面ADF,CE平面BEC,平面ADF∩平面BEC=OF,∴CE∥OF.
∵O是BE的中点,∴F是BC的中点.
(2)解 ∵BC与平面ABD所成角为30°,BC=AB=1,
∴C到平面ABD的距离为h=BC·sin 30°=![]() .
.
∵AE=2,∴VA-CDF=VF-ACD=![]() VB-ACD=
VB-ACD=![]() VC-ABD=
VC-ABD=![]() ×
×![]() ×
×![]() ×1×2×
×1×2×![]() =
=![]() .
.

练习册系列答案
相关题目