题目内容
【题目】已知抛物线C：y2＝2px(p>0)的准线方程为x＝－1，过定点M(m,0)(m>0)作斜率为k的直线l交抛物线C于A，B两点，E是M点关于坐标原点O的对称点，若直线AE和BE的斜率分别为k1，k2，则k1＋k2＝________.
【答案】0
【解析】依题意可知抛物线C的方程为y2＝4x，直线l的方程为y＝k(x－m)(k≠0，m>0)，
设A(x1，y1)，B(x2，y2)，由
消去x并整理得ky2－4y－4km＝0，
∴y1＋y2＝
，y1y2＝－4m，又E是M点关于坐标原点O的对称点，即有E（-m，0），
则k1＋k2＝
＝
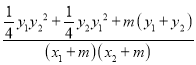
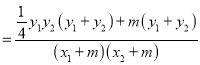
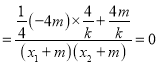
故答案为0
点睛: 本题考查抛物线的方程和性质，直线方程和抛物线方程联立，运用韦达定理，直线的斜率公式，注意点满足抛物线的方程，考查化简整理的运算能力，属于中档题．
练习册系列答案
相关题目
