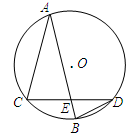题目内容
已知椭圆C:
+
=1(a>b>0)的离心率e=
,点F为椭圆的右焦点,点A、B分别为椭圆的左、右顶点,点M为椭圆的上顶点,且满足
•
=
-1.
(1)求椭圆C的方程;
(2)是否存在直线l,当直线l交椭圆于P、Q两点时,使点F恰为△PQM的垂心.若存在,求出直线l的方程;若不存在,请说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| MF |
| FB |
| 2 |
(1)求椭圆C的方程;
(2)是否存在直线l,当直线l交椭圆于P、Q两点时,使点F恰为△PQM的垂心.若存在,求出直线l的方程;若不存在,请说明理由.

(1)根据题意得,F(c,0),A(-a,0),B(a,0),M(0,b)
∴
=(c,-b),
=(a-c,0)
∴
•
=ac-c2=
-1(2分)
又e=
=
∴a=
c
∴
c2-c2=
-1
∴c2=1,a2=2,b2=1
∴椭圆C的方程为
+y2=1.(4分)
(2)假设存在直线l满足条件,使F是三角形MPQ的垂心.
因为KMF=-1,且FM⊥l,
所以k1=1,
所以设PQ直线y=x+m,
且设P(x1,y1),Q(x2),y2
由
消y,得3x2+4mx+2m2-2=0
△=16m2-12(2m2-2)>0,m2<3x1+x2=-
,x1x2=
.
y1y2=(x1+m)(x2+m)=x1x2+m(x1+x2)+m2=
-
+m2=
.(8分)
又F为△MPQ的垂心,
∴PF⊥MQ,∴
•
=0
又
(1-x1,-y1),
=(x2,y2-1)
∴
•
=x2+y1-x1x2-y1y2=x2+x1+m-x1x2-y1y2=-
m+m-
-
=0∴-
-m2+
=0,
∴3m2+m-4=0,m=-
,m=1(10分)
经检验满足m2<3(11分)
∴存在满足条件直线l方程为:x-y+1=0,3x-3y-4=0(12分)
∵x-y+1=0过M点 即MP重合 不构成三角形,
∴3x-3y-4=0满足题意.
∴
| MF |
| FB |
∴
| MF |
| FB |
| 2 |
又e=
| c |
| a |
| ||
| 2 |
∴a=
| 2 |
∴
| 2 |
| 2 |
∴c2=1,a2=2,b2=1
∴椭圆C的方程为
| x2 |
| 2 |
(2)假设存在直线l满足条件,使F是三角形MPQ的垂心.
因为KMF=-1,且FM⊥l,
所以k1=1,
所以设PQ直线y=x+m,
且设P(x1,y1),Q(x2),y2
由
|
消y,得3x2+4mx+2m2-2=0
△=16m2-12(2m2-2)>0,m2<3x1+x2=-
| 4m |
| 3 |
| 2m2-2 |
| 3 |
y1y2=(x1+m)(x2+m)=x1x2+m(x1+x2)+m2=
| 2m2-2 |
| 3 |
| 4m2 |
| 3 |
| m2-2 |
| 3 |
又F为△MPQ的垂心,
∴PF⊥MQ,∴
| PF |
| MQ |
又
| PF |
| MQ |
∴
| PF |
| MQ |
| 4 |
| 3 |
| 2m2-2 |
| 3 |
| m2-2 |
| 3 |
| m |
| 3 |
| 4 |
| 3 |
∴3m2+m-4=0,m=-
| 4 |
| 3 |
经检验满足m2<3(11分)
∴存在满足条件直线l方程为:x-y+1=0,3x-3y-4=0(12分)
∵x-y+1=0过M点 即MP重合 不构成三角形,
∴3x-3y-4=0满足题意.

练习册系列答案
相关题目
 的直径
的直径 的长为4,点
的长为4,点 平分弧
平分弧 ,过
,过 ,交
,交 .
. :
: 的角平分线,求
的角平分线,求 的长.
的长.
 AD,从AB的中点F作HF⊥EC于H.
AD,从AB的中点F作HF⊥EC于H.

 的直径
的直径 ,
, 是
是 延长线上的一点,过
延长线上的一点,过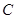 ,连接
,连接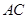 ,若
,若 ,
,
 .
.
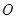 的两条弦, AB与CD相交于点E,且
的两条弦, AB与CD相交于点E,且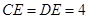 ,
,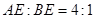 ,则
,则 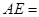 ______;
______;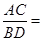 ______.
______.