题目内容
给定椭圆C:
+
=1(a>b>0),称圆心在坐标原点O,半径为
的圆是椭圆C的“伴随圆”,已知椭圆C的两个焦点分别是F1(-
,0),F2(
,0).
(1)若椭圆C上一动点M1满足|
|+|
|=4,求椭圆C及其“伴随圆”的方程;
(2)在(1)的条件下,过点P(0,t)(t<0)作直线l与椭圆C只有一个交点,且截椭圆C的“伴随圆”所得弦长为2
,求P点的坐标;
(3)已知m+n=-
,mn=-
(m≠n,θ∈(0,π)),是否存在a,b,使椭圆C的“伴随圆”上的点到过两点(m,m2),(n,n2)的直线的最短距离dmin=
.若存在,求出a,b的值;若不存在,请说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
| a2+b2 |
| 2 |
| 2 |
(1)若椭圆C上一动点M1满足|
| M1F1 |
| M1F2 |
(2)在(1)的条件下,过点P(0,t)(t<0)作直线l与椭圆C只有一个交点,且截椭圆C的“伴随圆”所得弦长为2
| 3 |
(3)已知m+n=-
| cosθ |
| sinθ |
| 3 |
| sinθ |
| a2+b2-b |
(1)由题意,c=
,a=2,∴b=
=
,所以椭圆C的方程为
+
=1.
其“伴随圆”的方程为x2+y2=6;
(2)设直线l的方程为y=kx+t,代入椭圆方程为(2k2+1)x2+4tkx+2t2-4=0
∴由△=(4tk)2-8(2k2+1)(t2-2)=0得t2=4k2+2①,
由直线l截椭圆C的“伴随圆”所得弦长为2
,可得
=
,即t2=3(k2+1)②
由①②可得t2=6.
∵t<0,∴t=-
,∴P(0,-
);
(3)过两点(m,m2),(n,n2)的直线的方程为
=
,∴y=(m+n)x-mn,
∵m+n=-
,mn=-
(m≠n,θ∈(0,π)),
∴y=-
x+
,得xcosθ+ysinθ-3=0,
∴由于圆心(0,0)到直线xcosθ+ysinθ-3=0的距离为d=
=3.
当a2+b2≥9时,dmin=0,但
-b>0,所以,等式不能成立;
当a2+b2<9时,dmin=3-
,由3-
=
-b得9+6b+b2=4a2+4b2.
因为a2=b2+2,所以7b2-6b-1=0,
∴(7b+1)(b-1)=0,∴b=1,a=
.
| 2 |
| a2-c2 |
| 2 |
| x2 |
| 4 |
| y2 |
| 2 |
其“伴随圆”的方程为x2+y2=6;
(2)设直线l的方程为y=kx+t,代入椭圆方程为(2k2+1)x2+4tkx+2t2-4=0
∴由△=(4tk)2-8(2k2+1)(t2-2)=0得t2=4k2+2①,
由直线l截椭圆C的“伴随圆”所得弦长为2
| 3 |
| |t| | ||
|
| 3 |
由①②可得t2=6.
∵t<0,∴t=-
| 6 |
| 6 |
(3)过两点(m,m2),(n,n2)的直线的方程为
| x-m |
| m-n |
| y-m2 |
| m2-n2 |
∵m+n=-
| cosθ |
| sinθ |
| 3 |
| sinθ |
∴y=-
| cosθ |
| sinθ |
| 3 |
| sinθ |
∴由于圆心(0,0)到直线xcosθ+ysinθ-3=0的距离为d=
| 3 | ||
|
当a2+b2≥9时,dmin=0,但
| a2+b2 |
当a2+b2<9时,dmin=3-
| a2+b2 |
| a2+b2 |
| a2+b2 |
因为a2=b2+2,所以7b2-6b-1=0,
∴(7b+1)(b-1)=0,∴b=1,a=
| 3 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 是圆
是圆 的直径,
的直径, 是圆
是圆 的切线,切点为
的切线,切点为 ,
, 平行于弦
平行于弦 ,若
,若 ,
, ,则
,则 .
.
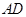 是⊙
是⊙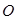 的直径,
的直径,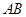 是⊙
是⊙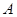 为切点,⊙
为切点,⊙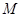 、
、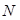 ,直线
,直线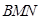 交
交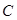 ,
,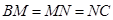 ,
,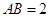 ,则⊙
,则⊙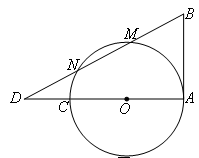
 为⊙
为⊙ 的两条切线,切点分别为
的两条切线,切点分别为 ,过
,过 的中点
的中点 作割线交⊙
作割线交⊙ 两点,若
两点,若 则
则 .
.