题目内容
如图所示,已知,在边长为1的正方形ABCD的一边上取一点E,使AE=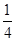 AD,从AB的中点F作HF⊥EC于H.
AD,从AB的中点F作HF⊥EC于H.

(1)求证:FH=FA;
(2)求EH∶HC的值.
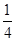 AD,从AB的中点F作HF⊥EC于H.
AD,从AB的中点F作HF⊥EC于H.
(1)求证:FH=FA;
(2)求EH∶HC的值.
(1)见解析 (2)1∶4
解:(1)证明:连接EF,FC,在正方形ABCD中,AD=AB=BC,∠A=∠B=90°.

∵AE=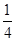 AD,F为AB的中点,
AD,F为AB的中点,
∴ =
= .
.
∴△EAF∽△FBC,
∴∠AEF=∠BFC,∠EFA=∠BCF.
又∠A=∠B=90°,
∴∠EFC=90°,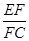 =
= .
.
又∵∠EFC=∠B=90°,∴△EFC∽△FBC.
∴∠HEF=∠BFC,∠ECF=∠BCF.
∴∠AEF=∠HEF,∠AFE=∠HFE,又EF=EF,
∴△EAF≌△EHF,∴FH=FA.
(2)由(1)知△EFC是直角三角形,FH是斜边EC上的高,
由射影定理可得EF2=EH·EC,FC2=CH·CE,于是EH∶HC=EF2∶FC2.
由(1)得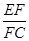 =
= ,于是EH∶HC=EF2∶FC2=1∶4.
,于是EH∶HC=EF2∶FC2=1∶4.

∵AE=
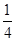 AD,F为AB的中点,
AD,F为AB的中点,∴
 =
= .
.∴△EAF∽△FBC,
∴∠AEF=∠BFC,∠EFA=∠BCF.
又∠A=∠B=90°,
∴∠EFC=90°,
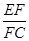 =
= .
.又∵∠EFC=∠B=90°,∴△EFC∽△FBC.
∴∠HEF=∠BFC,∠ECF=∠BCF.
∴∠AEF=∠HEF,∠AFE=∠HFE,又EF=EF,
∴△EAF≌△EHF,∴FH=FA.
(2)由(1)知△EFC是直角三角形,FH是斜边EC上的高,
由射影定理可得EF2=EH·EC,FC2=CH·CE,于是EH∶HC=EF2∶FC2.
由(1)得
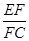 =
= ,于是EH∶HC=EF2∶FC2=1∶4.
,于是EH∶HC=EF2∶FC2=1∶4.
练习册系列答案
相关题目

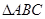 中,
中,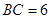 ,以
,以 为直径的半圆分别交
为直径的半圆分别交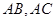 于点
于点 ,若
,若 ,则
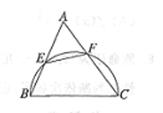
,则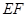 =_______.
=_______.

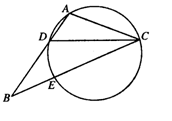
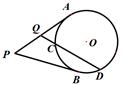
 为⊙
为⊙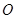 的两条切线,切点分别为
的两条切线,切点分别为 ,过
,过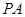 的中点
的中点 作割线交⊙
作割线交⊙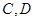 两点,若
两点,若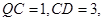 则
则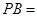 .
.
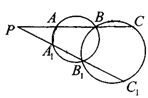
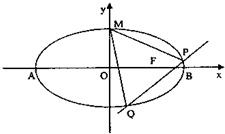
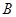 、
、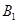 ,直线
,直线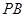 与
与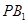 分别与两圆交于点
分别与两圆交于点 、
、 和
和 、
、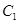 ,
,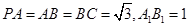 ,则
,则 .
.