题目内容
3.已知函数f(x)=sinxcosx+sinx+$\frac{2}{5}$cosx(0≤x≤$\frac{π}{2}$),则函数f(x)的最大值为( )| A. | 1 | B. | $\frac{7}{5}$ | C. | $\frac{38}{25}$ | D. | $\frac{43}{25}$ |
分析 三角换元令t=tan$\frac{x}{2}$∈[0,1],由万能公式可得f(x)=f(t)=$\frac{20t-2{t}^{4}+2}{5(1+{t}^{2})^{2}}$,由导数法判函数的单调性可得最值.
解答 解:∵0≤x≤$\frac{π}{2}$,∴t=tan$\frac{x}{2}$∈[0,1],
由万能公式可得f(x)=f(t)=$\frac{2t}{1+{t}^{2}}$•$\frac{1-{t}^{2}}{1+{t}^{2}}$+$\frac{2t}{1+{t}^{2}}$+$\frac{2}{5}$•$\frac{1-{t}^{2}}{1+{t}^{2}}$
=$\frac{2t(1-{t}^{2})}{(1+{t}^{2})^{2}}$+$\frac{10t+2(1-{t}^{2})}{5(1+{t}^{2})}$=$\frac{10t(1-{t}^{2})+10t(1+{t}^{2})+2(1-{t}^{4})}{5(1+{t}^{2})^{2}}$=$\frac{20t-2{t}^{4}+2}{5(1+{t}^{2})^{2}}$,
求导数可得f′(t)=$\frac{20-60{t}^{2}-8{t}^{3}-8t}{5(1+{t}^{2})^{3}}$,令f′(t)=0可得20-60t2-8t3-8t=0,
分解因式可得(t-$\frac{1}{2}$)(t2+8t+5)=0,∵t∈[0,1],∴t=$\frac{1}{2}$,
当0<t<$\frac{1}{2}$时,f′(t)>0,函数f(t)单调递增,当$\frac{1}{2}$<t<1时,f′(t)<0,函数f(t)单调递减,
∴f(x)的最大值即f(t)的最大值为f($\frac{1}{2}$)=$\frac{38}{25}$,
故选:C
点评 本题考查导数法求函数的最值,三角换元是解决问题的关键,属中档题.

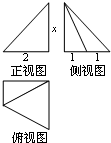 某几何体的三视图如图所示,且该几何体的体积是6,则正视图中的x的值是( )
某几何体的三视图如图所示,且该几何体的体积是6,则正视图中的x的值是( )| A. | 9 | B. | 8 | C. | 3 | D. | 6 |
 如图是一个几何体的三视图,根据图中数据,求该几何体的表面积和体积.
如图是一个几何体的三视图,根据图中数据,求该几何体的表面积和体积.
