题目内容
8.已知射线OA,OB的方程分别为y=$\frac{\sqrt{3}}{3}$x(x≥0),y=-$\frac{\sqrt{3}}{3}$x(x≤0),动点M、N分别在OA、OB上滑动,且MN=4$\sqrt{3}$.(1)若$\overrightarrow{MP}$=$\overrightarrow{PN}$,求点P的轨迹C的方程;
(2)已知F1(-4$\sqrt{2}$,0),F2(4$\sqrt{2}$,0),请问:在曲线C上是否存在动点P满足条件$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0?若存在,求出点P的坐标,若不存在,请说明理由.
分析 (1)先设出M,N,P三点的坐标,M(${x}_{1},\frac{\sqrt{3}}{3}{x}_{1}$),N(${x}_{2},-\frac{\sqrt{3}}{3}{x}_{2}$),P(x,y),由中点坐标公式可得到${x}_{1}+{x}_{2}=2x,{x}_{1}-{x}_{2}=2\sqrt{3}y$,将这两个式子带入|MN|=$\sqrt{({x}_{1}-{x}_{2})^{2}+\frac{1}{3}({x}_{1}+{x}_{2})^{2}}$,然后化简即可得到点P的轨迹方程为$\frac{{x}^{2}}{36}+\frac{{y}^{2}}{4}=1$;
(2)由上面便知轨迹为椭圆,并且F1,F2是它的两个焦点,根据$\overrightarrow{P{F}_{1}}•\overrightarrow{P{F}_{2}}=0$便知PF1⊥PF2,所提的问题便可说成在曲线C上是否存在动点P,使PF1⊥PF2.根据椭圆的特点,只需验证椭圆的上顶点和焦点的连线的夹角是否大于等于90°即可,可设上顶点为Q,根据余弦定理即可求出cos∠F1QF2并判断该余弦值是否小于等于0即可.当存在满足条件的P点时,可设出P点的坐标(x0,y0),然后根据P点在椭圆上,和$\overrightarrow{P{F}_{1}}•\overrightarrow{P{F}_{2}}=0$便可建立关于x0,y0的方程,解方程即可求得P点坐标.
解答 解:(1)根据已知条件设M(${x}_{1},\frac{\sqrt{3}}{3}{x}_{1}$),N(${x}_{2},-\frac{\sqrt{3}}{3}{x}_{2}$),P(x,y);
∵$\overrightarrow{MP}=\overrightarrow{PN}$;
∴P为MN的中点;
∴根据中点坐标公式$\left\{\begin{array}{l}{x=\frac{{x}_{1}+{x}_{2}}{2}}\\{y=\frac{\sqrt{3}}{6}({x}_{1}-{x}_{2})}\end{array}\right.$;
∴$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=2x}\\{{x}_{1}-{x}_{2}=2\sqrt{3}y}\end{array}\right.$①;
∵$|MN|=4\sqrt{3}$;
∴$\sqrt{({x}_{1}-{x}_{2})^{2}+\frac{1}{3}({x}_{1}+{x}_{2})^{2}}=4\sqrt{3}$;
带入①并两边平方得:
$12{y}^{2}+\frac{4}{3}{x}^{2}=48$;
化简得$\frac{{x}^{2}}{36}+\frac{{y}^{2}}{4}=1$;
(2)由轨迹C的方程知点P的轨迹是椭圆,并且F1,F2分别是该椭圆的左右焦点;
$\overrightarrow{P{F}_{1}}•\overrightarrow{PF}=0$;
∴$\overrightarrow{P{F}_{1}}⊥\overrightarrow{P{F}_{2}}$;
∴就是判断是否在曲线C上存在点P,使PF1⊥PF2;
如图,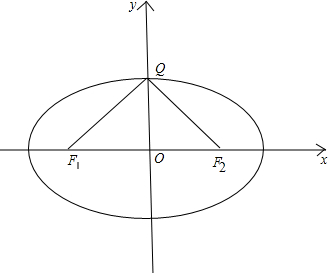
椭圆的上下顶点和焦点的连线所夹的角是椭圆上其它点和焦点连线夹角的最大值;
设椭圆上顶点为Q,只要∠F1QF2≥90°,在椭圆上便存在点P,使PF1⊥PF2;
$|Q{F}_{1}|=|Q{F}_{2}|=6,|{F}_{1}{F}_{2}|=8\sqrt{2}$;
∴根据余弦定理$cos∠{F}_{1}Q{F}_{2}=\frac{36+36-128}{72}<0$;
∴∠F1PF2为钝角;
∴在椭圆上存在点P,使PF1⊥PF2,即$\overrightarrow{P{F}_{1}}•\overrightarrow{P{F}_{2}}=0$;
设P(x0,y0),P点在椭圆上,且满足$\overrightarrow{P{F}_{1}}•\overrightarrow{P{F}_{2}}=0$,;
所以得到$\left\{\begin{array}{l}{\frac{{{x}_{0}}^{2}}{36}+\frac{{{y}_{0}}^{2}}{4}=1}\\{{{x}_{0}}^{2}-32+{{y}_{0}}^{2}=0}\end{array}\right.$;
解得${x}_{0}=±\frac{3\sqrt{14}}{2},{y}_{0}=±\frac{\sqrt{2}}{2}$;
∴符合条件的P点坐标为:$(\frac{3\sqrt{14}}{2},\frac{\sqrt{2}}{2}),(\frac{3\sqrt{14}}{2},-\frac{\sqrt{2}}{2})$,$(-\frac{3\sqrt{14}}{2},\frac{\sqrt{2}}{2}),(-\frac{3\sqrt{14}}{2},-\frac{\sqrt{2}}{2})$.
点评 考查轨迹方程的求解过程,两点间距离公式,中点坐标公式,以及椭圆的标准方程,椭圆的焦点、焦距,和短半轴的概念,两非零向量垂直的充要条件,余弦定理,以及知道椭圆的上下顶点和焦点的连线的夹角是椭圆上其它点与焦点连线所成夹角中是最大的.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 1 | B. | $\frac{7}{5}$ | C. | $\frac{38}{25}$ | D. | $\frac{43}{25}$ |