题目内容
1.在下列四个函数中,在(0,+∞)为增函数的是( )| A. | y=3-x | B. | y=x2-3x | C. | $f(x)={(\frac{1}{2})^x}$ | D. | f(x)=|x| |
分析 分别根据基本初等函数的单调性判断出正确答案.
解答 解:A、函数y=3-x在R上是减函数,A不符合题意;
B、函数y=x2-3x在($\frac{3}{2}$,+∞)是增函数,在($-∞,\frac{3}{2}$)上是减函数,B不符合题意;
C、函数$f(x)={(\frac{1}{2})}^{x}$在R上是减函数,C不符合题意;
D、∵f(x)=|x|=$\left\{\begin{array}{l}{x,x≥0}\\{-x,x<0}\end{array}\right.$,∴在(0,+∞)为增函数,D符合题意,
故选:D.
点评 本题考查基本初等函数的单调性,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.若等比数列{an}满足log3a1+log3a2+…+log3a10=10,则a2a9+a4a7的值为( )
| A. | 9 | B. | 18 | C. | 27 | D. | 2+log35 |
16.已知条件p:x>1,q:$\frac{1}{x}$<1,则¬p是¬q成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
10.偏差是指个别测定值与测定的平均值之差,在成绩统计中,我们把某个同学的某科考试成绩与该科班平均分的差叫某科偏差,在某次考试成绩统计中,某老师为了对学生数学偏差x(单位:分)与物理偏差y(单位:分)之间的关系进行分析,随机挑选了8位同学,得到他们的两科成绩偏差数据如下:
(Ⅰ)若x与y之间具有线性相关关系,求y关于x的线性回归方程;
(Ⅱ)若该次考试该班数学平均分为120分,物理平均分为91.5分,试由(1)的结论预测数学成绩为128分的同学的物理成绩.
参考数据:
$\sum_{i=1}^{8}$xiyi=20×6.5+15×3.5+13×3.5+3×1.5+2×0.5+(-5)×(-0.5)+(-10)×(-2.5)+(-18)×(-3.5)=324
$\sum_{i=1}^{8}$x${\;}_{i}^{2}$=202+152+132+32+22+(-5)2+(-10)2+(-18)2=1256.
| 学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学偏差x | 20 | 15 | 13 | 3 | 2 | -5 | -10 | -18 |
| 物理偏差y | 6.5 | 3.5 | 3.5 | 1.5 | 0.5 | -0.5 | -2.5 | -3.5 |
(Ⅱ)若该次考试该班数学平均分为120分,物理平均分为91.5分,试由(1)的结论预测数学成绩为128分的同学的物理成绩.
参考数据:
$\sum_{i=1}^{8}$xiyi=20×6.5+15×3.5+13×3.5+3×1.5+2×0.5+(-5)×(-0.5)+(-10)×(-2.5)+(-18)×(-3.5)=324
$\sum_{i=1}^{8}$x${\;}_{i}^{2}$=202+152+132+32+22+(-5)2+(-10)2+(-18)2=1256.
11.若将字母o,o,r,t随机排列,则排得root的概率为( )
| A. | $\frac{1}{24}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{2}$ |
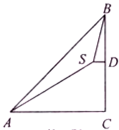 如图,在山底A处测得山顶B的仰角∠CAB=45°,沿倾斜角为30°的斜坡AS走2000米至S点,又测得山顶∠DSB=75°,则山高BC为2000米.
如图,在山底A处测得山顶B的仰角∠CAB=45°,沿倾斜角为30°的斜坡AS走2000米至S点,又测得山顶∠DSB=75°,则山高BC为2000米.