题目内容
17.已知|$\overrightarrow{a}$|=4,|$\overrightarrow{b}$|=3,且向量$\overrightarrow{a}$与$\overrightarrow{b}$互相垂直.(Ⅰ)若向量$\overrightarrow{c}$=3k$\overrightarrow{a}$+4k$\overrightarrow{b}$(k∈R),且|$\overrightarrow{c}$|=12$\sqrt{2}$,求|k|的值;
(Ⅱ)若向量$\overrightarrow{c}$满足($\overrightarrow{a}-\overrightarrow{c}$)$⊥(\overrightarrow{c}-\overrightarrow{b})$,求|$\overrightarrow{c}$|的取值范围.
分析 (Ⅰ)建立坐标系设出$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$坐标,用|$\overrightarrow{c}$|=12$\sqrt{2}$,求出|k|的值;
(Ⅱ)利用向量垂直数量积为0,得到$\overrightarrow{c}$的坐标关系式,利用其几何意义求最值.
解答 解:据题意:建立坐标系.不妨设$\overrightarrow{a}$=(4,0),$\overrightarrow{b}$=(0,3),------(2分)
(Ⅰ) 向量$\overrightarrow{c}$=3k$\overrightarrow{a}$+4k$\overrightarrow{b}$=(12k,12k)
∴|$\overrightarrow{c}$|=$\sqrt{(12k)^{2}+(12k)^{2}}$=12$\sqrt{2}$,------(4分)
解得|k|=1-----(6分)
(Ⅱ) 设$\overrightarrow{c}$=(x,y),则 由($\overrightarrow{a}-\overrightarrow{c}$)$⊥(\overrightarrow{c}-\overrightarrow{b})$,得到($\overrightarrow{a}-\overrightarrow{c}$)$•(\overrightarrow{c}-\overrightarrow{b})$=(4-x)x-(y-3)y=0,------(8分)
即(x-2)2+(y-1.5)2=6.25.------(10分)
由此可以判定,向量$\overrightarrow{c}$的起点在原点,终点在以(2,1.5)为圆心,半径为2.5的圆上,注意到原点也在此圆上,
所以,|$\overrightarrow{c}$|的取值范围[0,5].------(12分)
点评 本题考查了平面向量的坐标运算、模的计算以及向量垂直的性质运用,用到了几何意义求模的范围;属于中档题.

| A. | $\frac{3π+6}{4}$ | B. | $\frac{3π+4}{4}$ | C. | π+1 | D. | $\frac{3π+3}{2}$ |
| A. | 0.4 | B. | 0.2 | C. | 0.1 | D. | 0.05 |
| A. | 1 | B. | 2 | C. | sin1 | D. | 2sin1 |
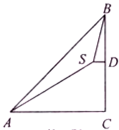 如图,在山底A处测得山顶B的仰角∠CAB=45°,沿倾斜角为30°的斜坡AS走2000米至S点,又测得山顶∠DSB=75°,则山高BC为2000米.
如图,在山底A处测得山顶B的仰角∠CAB=45°,沿倾斜角为30°的斜坡AS走2000米至S点,又测得山顶∠DSB=75°,则山高BC为2000米.