题目内容
【题目】已知函数![]() .
.
(1)当![]() ,
,![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(2)对于任意![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的最大值.
的最大值.
【答案】见解析
【解析】(1)当![]() 时,
时,![]() ,其定义域为
,其定义域为![]() ,
,
![]() .…………………1分
.…………………1分
令![]() ,
,![]() .
.
①当![]() 时,
时,![]() 恒成立,
恒成立,
故![]() 恒成立,故
恒成立,故![]() 在
在![]() 上为增函数;…………………2分
上为增函数;…………………2分
②当![]() 时,
时,![]() ,令
,令![]() ,得
,得![]() (
(![]() ),
),
当![]() 时,
时,![]() ,
,![]() 为增函数,当
为增函数,当![]() 时,
时,![]() ,
,![]() 为减函数,当
为减函数,当![]() 时,
时,![]() ,
,![]() ,
,![]() 为增函数,…………………4分
为增函数,…………………4分
综上,当![]() 时,
时,![]() 在
在![]() 上为增函数;当
上为增函数;当![]() 时,
时,![]() 在
在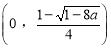 ,
,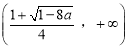 上为增函数,在
上为增函数,在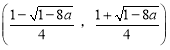 上为减函数.…………………5分
上为减函数.…………………5分
(2)不等式等价于![]() ,
,
即![]() 等价于
等价于![]() .…………………6分
.…………………6分
令![]() ,
,![]() ,则
,则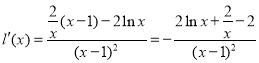 .…………………7分
.…………………7分
再令![]() ,
,![]() ,则
,则![]() ,
,
故![]() 在
在![]() 上为减函数,于是
上为减函数,于是![]() ,…………………9分
,…………………9分
从而![]() ,于是
,于是![]() 在
在![]() 上为减函数,所以
上为减函数,所以![]() ,…………………10分
,…………………10分
故要使![]() 恒成立,只要
恒成立,只要![]() .…………………11分
.…………………11分
综上,![]() 的最大值为
的最大值为![]() .…………………12分
.…………………12分
请考生在第22、23两题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做的第一个题目计分.
【命题意图】本题主要考查利用导数研究函数的单调性、不等式恒成立等基础知识,意在考查逻辑推理能
力、等价转化能力、运算求解能力,以及考查函数与方程思想、分类讨论思想.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目

