题目内容
【题目】在平面直角坐标系中,圆![]() :
: ![]() 与
与![]() 轴的正半轴交于点
轴的正半轴交于点![]() ,以
,以![]() 为圆心的圆
为圆心的圆![]() :
: ![]() (
(![]() )与圆
)与圆![]() 交于
交于![]() ,
, ![]() 两点.
两点.
(1)若直线![]() 与圆
与圆![]() 切于第一象限,且与坐标轴交于
切于第一象限,且与坐标轴交于![]() ,
, ![]() ,当直线
,当直线![]() 长最小时,求直线
长最小时,求直线![]() 的方程;
的方程;
(2)设![]() 是圆
是圆![]() 上异于
上异于![]() ,
, ![]() 的任意一点,直线
的任意一点,直线![]() 、
、![]() 分别与
分别与![]() 轴交于点
轴交于点![]() 和
和![]() ,问
,问![]() 是否为定值?若是,请求出该定值;若不是,请说明理由.
是否为定值?若是,请求出该定值;若不是,请说明理由.

【答案】(1)![]() (2)是定值,定值为4
(2)是定值,定值为4
【解析】试题分析:(1)先设出直线的截距式方程![]() ,利用直线
,利用直线![]() 与圆
与圆![]() 相切,则圆心到直线的距离等于半径列出关于
相切,则圆心到直线的距离等于半径列出关于![]() 的等式
的等式![]() ,由于
,由于![]() ,利用基本不等式可以得到
,利用基本不等式可以得到![]() 时,线段
时,线段![]() 长最小,写出直线方程即可;(2)先设出
长最小,写出直线方程即可;(2)先设出![]() ,
, ![]() ,从而得到
,从而得到![]() ,以及直线PB、PC的方程,分别令
,以及直线PB、PC的方程,分别令![]() ,得到点M与点N的横坐标
,得到点M与点N的横坐标![]()
![]()
![]() ,再利用点B、P在圆上进行化简即可;
,再利用点B、P在圆上进行化简即可;
试题解析:(1)设直线![]() 的方程为
的方程为![]() ,即
,即![]() ,由直线
,由直线![]() 与圆
与圆![]() 相切,得
相切,得![]() ,即
,即![]() ,
, ![]() ,
,
当且仅当![]() 时取等号,此时直线
时取等号,此时直线![]() 的方程为
的方程为![]() .
.
(2)设![]() ,
, ![]() ,则
,则![]() ,
, ![]() ,
, ![]()
直线![]() 的方程为:
的方程为: ![]()
直线![]() 的方程为:
的方程为: ![]()
分别令![]() ,得
,得![]()
所以![]()
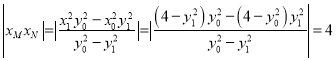 为定值.
为定值.

练习册系列答案
相关题目
