题目内容
【题目】已知奇函数f(x)= ![]() 的定义域为[﹣a﹣2,b]
的定义域为[﹣a﹣2,b]
(1)求实数a,b的值;
(2)判断函数f(x)的单调性,并用定义给出证明;
(3)若实数m满足f(m﹣1)<f(1﹣2m),求m的取值范围.
【答案】
(1)∵f(x)是奇函数,故f(0)=0,
即a﹣1=0,解得:a=1,故﹣a﹣2=﹣3,
定义域为[﹣a﹣2,b],关于原点对称,
故b=3
(2)函数f(x)在[﹣3,3]递增,
证明如下:设x1,x2是[﹣3,3]上的任意2个值,且x1<x2,
则f(x1)﹣f(x2)= ![]() ﹣
﹣ ![]() =
= 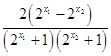 ,
,
∵﹣3≤x1<x2≤3,∴ ![]() ﹣
﹣ ![]() <0,又
<0,又 ![]() +1>0,
+1>0, ![]() +1>0,
+1>0,
∴f(x1)﹣f(x2)<0,即f(x1)<f(x2),
∴f(x)在[﹣3,3]递增
(3)由(1)得f(x)在[﹣3,3]递增,
∴f(m﹣1)<f(1﹣2m)等价于:
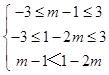 ,解得:﹣1≤m<
,解得:﹣1≤m< ![]() ,
,
故不等式的解集是[﹣1, ![]() )
)
【解析】(1)根据函数的奇偶性求出a,b的值即可;(2)根据函数单调性的定义证明即可;(3)根据函数的单调性以及函数的定义域得到关于m的不等式组,解出即可.
【考点精析】通过灵活运用函数单调性的判断方法和函数奇偶性的性质,掌握单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较;在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇即可以解答此题.

 阅读快车系列答案
阅读快车系列答案【题目】为评估设备![]() 生产某种零件的性能,从设备
生产某种零件的性能,从设备![]() 生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:
生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:
直径/ | 58 | 59 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 73 | 合计 |
件数 | 1 | 1 | 3 | 5 | 6 | 19 | 33 | 18 | 4 | 4 | 2 | 1 | 2 | 1 | 100 |
经计算,样本的平均值![]() ,标准差
,标准差![]() ,以频率值作为概率的估计值.
,以频率值作为概率的估计值.
(1)为评判一台设备的性能,从该设备加工的零件中任意抽取一件,记其直径为![]() ,并根据以下不等式进行评判(
,并根据以下不等式进行评判(![]() 表示相应事件的概率);
表示相应事件的概率);
①![]() ;
;
②![]() ;
;
③![]()
评判规则为:若同时满足上述三个不等式,则设备等级为甲;仅满足其中两个,则等级为乙;若仅满足其中一个,则等级为丙;若全部不满足,则等级为丁,试判断设备![]() 的性能等级.
的性能等级.
(2)将直径小于等于![]() 或直径大于
或直径大于![]() 的零件认为是次品.
的零件认为是次品.
①从设备![]() 的生产流水线上随意抽取2件零件,计算其中次品个数
的生产流水线上随意抽取2件零件,计算其中次品个数![]() 的数学期望
的数学期望![]() ;
;
②从样本中随意抽取2件零件,计算其中次品个数![]() 的数学期望
的数学期望![]() .
.