题目内容
【题目】已知定义在R上的偶函数f（x），当x∈（﹣∞，0]时的解析式为f（x）=x2+2x
（1）求函数f（x）在R上的解析式；
（2）画出函数f（x）的图象并直接写出它的单调区间．
【答案】
（1）解：当x＞0时，﹣x＜0，f（﹣x）=（﹣x）2﹣2x=x2﹣2x
又f（x）为偶函数，∴f（﹣x）=f（x）
∴f（x）=x2﹣2x
∴ 
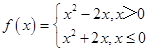
（2）解： 
单调递增区间为：（﹣1，0），（1，+∞）
单调递减区间为：（0，1），（﹣∞，﹣1）
【解析】（1）由已知中，x∈（﹣∞，0]时的解析式为f（x）=x2+2x，我们可由x＞0时，﹣x＜0，代入求出f（﹣x），进而根据y=f（x）是偶函数，得到x＞0时，f（x）的解析式；（2）根据分段函数分段画的原则，结合（1）中函数的解析式，我们易画出函数的图象，结合图象，我们根据从左到右图象上升，函数为增函数，图象下降，函数为减函数的原则，得到函数的单调性．
【考点精析】解答此题的关键在于理解奇偶性与单调性的综合的相关知识，掌握奇函数在关于原点对称的区间上有相同的单调性；偶函数在关于原点对称的区间上有相反的单调性．
练习册系列答案
相关题目
