题目内容
15．设关于x的不等式|x+5|+|x-5|≤a（1）当a=12时，解这个不等式；
（2）当a为何值时，这个不等式的解集为∅．
分析 （1）令y=|x+5|+|x-5|=$\left\{\begin{array}{l}{-2x，x≤-5}\\{10，-5＜x≤5}\\{2x，x＞5}\end{array}\right.$，作出函数y的图象，数形结合求得f（x）≤12 的解集．
（2）由函数f（x）的解析式求得它的最小值，可得满足条件的a的范围．
解答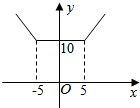 
解：（1）令y=|x+5|+|x-5|=$\left\{\begin{array}{l}{-2x，x≤-5}\\{10，-5＜x≤5}\\{2x，x＞5}\end{array}\right.$，
作出函数y的图象，如图所示：
当a=12时，不等式即f（x）≤12，令f（x）=12，求得x=±6，
可得f（x）≤12 的解集为[-6，6]．
（2）由于函数f（x）|=$\left\{\begin{array}{l}{-2x，x≤-5}\\{10，-5＜x≤5}\\{2x，x＞5}\end{array}\right.$ 的最小值为10，故当a＜10时，
不等式|x+5|+|x-5|≤a的解集为∅．
点评 本题主要考查对由绝对值的函数，绝对值不等式的解法，体现了转化、数形结合的数学思想，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
5．已知动点M的坐标满足方程5$\sqrt{{x}^{2}+{y}^{2}}$=|3x+4y-12|，则动点M的轨迹是（ ）
| A． | 椭圆 | B． | 抛物线 | C． | 双曲线 | D． | 以上都不对 |
6．若抛物线C1：y2=2px（p＞0）的焦点F恰好是双曲C2：$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的右焦点，且它们的交点的连线过点F，则双曲线的离心率为（ ）
| A． | $\sqrt{2}+1$ | B． | $\frac{{\sqrt{5}}}{2}$ | C． | $\frac{{\sqrt{6}+\sqrt{2}}}{2}$ | D． | $\frac{{\sqrt{2}+1}}{2}$ |
10．若不等式|a-2x|≤x+3对任意x∈[0，2]恒成立，则实数a的取值范围是（ ）
| A． | （-1，3） | B． | [-1，3] | C． | （1，3） | D． | [1，3] |