题目内容
10.若不等式|a-2x|≤x+3对任意x∈[0,2]恒成立,则实数a的取值范围是( )| A. | (-1,3) | B. | [-1,3] | C. | (1,3) | D. | [1,3] |
分析 由题意可得f(x)=|a-2x|的图象在x∈[0,2]上恒位于直线y=x+3的下方或在直线y=x+3上,数形结合可得$\left\{\begin{array}{l}{\frac{a}{2}<0}\\{f(2)=|4-a|≤5}\end{array}\right.$ ①,或 $\left\{\begin{array}{l}{\frac{a}{2}≥0}\\{f(2)=|a-4|≤5}\\{f(0)=|a|≤3}\end{array}\right.$ ②,分别求得①、②的解集,再取并集,即得所求.
解答 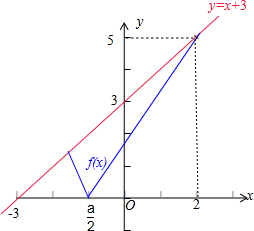 解:由不等式|a-2x|≤x+3对任意x∈[0,2]上恒成立,
解:由不等式|a-2x|≤x+3对任意x∈[0,2]上恒成立,
可得f(x)=|a-2x|的图象在x∈[0,2]上恒位于直线y=x+3的下方或在直线y=x+3上,
如图所示:
∴$\left\{\begin{array}{l}{\frac{a}{2}<0}\\{f(2)=|4-a|≤5}\end{array}\right.$ ①,或 $\left\{\begin{array}{l}{\frac{a}{2}≥0}\\{f(2)=|a-4|≤5}\\{f(0)=|a|≤3}\end{array}\right.$ ②.
由①可得-1≤a<0,由②可得0≤a≤3,
故实数a的取值范围是{a|-1≤a<0,或者0≤a≤3}=[-1,3],
故选:B.
点评 本题主要考查绝对值不等式的解法,函数的恒成立问题,体现了数形结合、分类讨论的数学思想,属于中档题.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
20.已知在△ABC中,a=$\sqrt{5},b=\sqrt{15},A={30°}$,则c等于( )
| A. | 2$\sqrt{5}$ | B. | $\sqrt{5}$或2$\sqrt{5}$ | C. | $\sqrt{15}$ | D. | 以上都不对 |
2.已知对于任意实数a(a>0,且a≠1),函数f(x)=7+ax-1的图象恒过点P,则P点的坐标是( )
| A. | (1,8) | B. | (1,7) | C. | (0,8) | D. | (8,0) |
19.某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
(Ⅰ)求线性回归方程$\widehat{y}$=bx+a;
(Ⅱ)预计在今后的销售中,销量与单价仍然服从(Ⅰ)中的关系,且该产品的成本是3.5元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本).
(参考公式与数据:$\sum_{i=1}^{6}$xiyi=4066,$\sum_{i=1}^{6}$x${\;}_{i}^{2}$=434.2,$\sum_{i=1}^{6}$xi=51.$\sum_{i=1}^{6}$yi=480.$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.)
| 单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
(Ⅱ)预计在今后的销售中,销量与单价仍然服从(Ⅰ)中的关系,且该产品的成本是3.5元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本).
(参考公式与数据:$\sum_{i=1}^{6}$xiyi=4066,$\sum_{i=1}^{6}$x${\;}_{i}^{2}$=434.2,$\sum_{i=1}^{6}$xi=51.$\sum_{i=1}^{6}$yi=480.$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.)
20.在等比数列{an}中,a1=2,a4=$\frac{1}{4}$.若am=2-15,则m=( )
| A. | 17 | B. | 16 | C. | 14 | D. | 13 |
 根据某电子商务平台的调查统计显示,参与调查的1000位上网购物者的年龄情况如图显示.
根据某电子商务平台的调查统计显示,参与调查的1000位上网购物者的年龄情况如图显示.