题目内容
3.若a、b分别是方程x+lgx=4,x+10x=4的解,$f(x)=\left\{{\begin{array}{l}{\frac{a+b}{x}+2,x<0}\\{2,x>0}\end{array}}\right.$.则关于x的方程f(x)=2x-1的解的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由题意可得a=104-a,4-b=10b,再作出函数y=4-x与y=10x的图象,从而可得a+b=4;从而解得.
解答 解:∵a、b分别是方程x+lgx=4,x+10x=4的解,
∴a+lga=4,b+10b=4,
∴a=104-a,4-b=10b,
作函数y=4-x与y=10x的图象如下,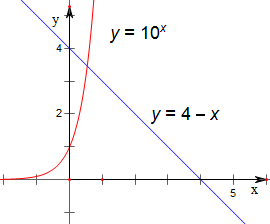
结合图象可知,有且仅有一个交点,
故a=4-b,
即a+b=4;
①当x<0时,方程f(x)=2x-1可化为$\frac{4}{x}$+2=2x-1,
解得,x=$\frac{3-\sqrt{41}}{4}$;
②当x>0时,方程f(x)=2x-1可化为2=2x-1,
解得,x=$\frac{3}{2}$;
故关于x的方程f(x)=2x-1的解的个数是2,
故选B.
点评 本题考查了对数函数与指数函数的互化与应用,同时考查了数形结合的思想应用,属于中档题.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
11.正方体ABCD-A1B1C1D1中,异面直线AA1与BC1所成的角为( )
| A. | 60° | B. | 45° | C. | 30° | D. | 90° |
8.已知等差数列{an}中,3a5+7a11=5,Sn是{an}的前n项和,则S9+S21=( )
| A. | 5 | B. | 10 | C. | 15 | D. | 20 |
 根据某电子商务平台的调查统计显示,参与调查的1000位上网购物者的年龄情况如图显示.
根据某电子商务平台的调查统计显示,参与调查的1000位上网购物者的年龄情况如图显示.