题目内容
【题目】如图,在以![]() 为顶点的五面体中,O为AB的中点,
为顶点的五面体中,O为AB的中点,
![]() 平面
平面![]() ,
, ![]() ∥
∥![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(1)在图中过点O作平面![]() ,使得
,使得![]() ∥平面
∥平面![]() ,并说明理由;
,并说明理由;
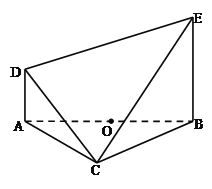
(2)求直线DE与平面CBE所成角的正切值.
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)在BE上取点F,使得![]() ,在BC上取点H,使
,在BC上取点H,使![]() ,平面OFH即为所求的平面
,平面OFH即为所求的平面![]() 取BE的中点G,连接AG,再证明
取BE的中点G,连接AG,再证明![]() ∥平面
∥平面![]() 即可;(2)先证明
即可;(2)先证明![]() 是
是![]() 与平面
与平面![]() 所成的角,根据
所成的角,根据![]() 与平面
与平面![]() 所成的角等于
所成的角等于![]() 与平面
与平面![]() 所成的角,利用直角三角形性质可得结果.
所成的角,利用直角三角形性质可得结果.
试题解析:(1)如图,在BE上取点F,使得![]() ,在BC上取点H,使
,在BC上取点H,使![]() ,连接OF,FH,OH,则平面OFH即为所求的平面
,连接OF,FH,OH,则平面OFH即为所求的平面![]() .
.
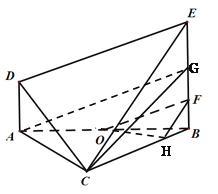
理由如下:
取BE的中点G,连接AG,
![]() ,
, ![]() 为
为![]() 中点,
中点, ![]()
![]() ∥
∥![]()
![]() ∥
∥![]() ,
, ![]() 是平行四边形,
是平行四边形,
![]()
![]() ∥
∥![]()
![]() 中,
中, ![]() 是
是![]() 中点,
中点, ![]() 是
是![]() 中点,
中点,
所以![]() 是中位线,
是中位线,![]() ∥
∥![]()
![]() ∥
∥![]() ,
,
![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
![]() ∥平面
∥平面![]() .
.
又![]() 中,
中, ![]() ,
, ![]() ,
,
![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
又![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
![]() 平面
平面![]() 平面
平面![]() ,即
,即![]() ∥平面
∥平面![]() .
.
(2)连接![]() ,因为
,因为![]() 平面
平面![]() ,
,
又![]() ∥
∥![]() ,所以
,所以![]() 平面
平面![]() ,
, ![]()
又![]()
![]() 平面
平面![]()
![]() 是
是![]() 与平面
与平面![]() 所成的角,
所成的角,
![]() ∥
∥![]() ,
,
![]()
![]() 与平面
与平面![]() 所成的角等于
所成的角等于![]() 与平面
与平面![]() 所成的角
所成的角
在![]() 中,
中, ![]() ,
, ![]() ,
, ![]()
![]() 在
在![]() 中,
中, ![]()
![]() 在
在![]() 中,
中, ![]()
即直线DE与平面CBE所成角的正切值为![]()

练习册系列答案
相关题目