题目内容
【题目】已知函数![]() ,且直线
,且直线![]() 是函数
是函数![]() 的一条切线.
的一条切线.
(1)求![]() 的值;
的值;
(2)对任意的![]() ,都存在
,都存在![]() ,使得
,使得![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)已知方程![]() 有两个根
有两个根![]() ,若
,若![]() ,求证:
,求证: ![]() .
.
【答案】(1) ![]() ;(2)
;(2) ![]() ;(3) 详见解析.
;(3) 详见解析.
【解析】试题分析:(1)对函数![]() 求导,
求导, ![]() ,设直线
,设直线![]() 与函数
与函数![]() 相切与点
相切与点![]() ,根据导数的几何意义可得,
,根据导数的几何意义可得, 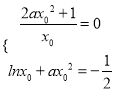 ,解得
,解得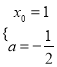 ,求出
,求出![]() ;(2)对任意的
;(2)对任意的![]()
![]() ,都存在
,都存在![]() ,使得
,使得![]() ,只需要
,只需要![]() 的值域是
的值域是![]() 值域的子集,利用导数的方法分别求
值域的子集,利用导数的方法分别求![]() 、
、![]() 的值域,即可求出
的值域,即可求出![]() 的取值范围;(3)根据题意得
的取值范围;(3)根据题意得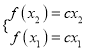 ,两式相减得,
,两式相减得, ![]() ,所以
,所以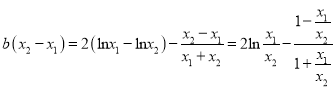 ,令
,令![]() ,则
,则![]() ,则
,则![]() ,令
,令![]() ,对
,对![]() 求导,判断
求导,判断![]() 的单调,证明
的单调,证明![]() .
.
试题解析:(1)设直线![]() 与
与![]() 相切于点
相切于点![]() ,依题意得
,依题意得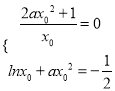 ,解得
,解得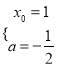 ,所以
,所以![]() ,经检验:
,经检验: ![]() 符合题意.
符合题意.
(2) 由(1)得![]() ,所以
,所以![]() ,当
,当![]() ,
, ![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 上单调递减,所以当
上单调递减,所以当![]() ,
, ![]() 时,
时, ![]()
![]()
![]() ,
, ![]() ,当
,当![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 上单调递增,所以当
上单调递增,所以当![]() 时,
时, ![]() ,依题意得
,依题意得![]()
![]() ,所以
,所以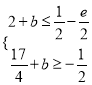 ,解得
,解得![]() .
.
(3) 依题意得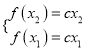 ,两式相减得
,两式相减得![]() ,所以
,所以![]() ,方程
,方程![]() 可转化为
可转化为![]() ,即
,即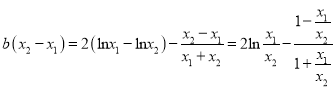 ,令
,令![]() ,则
,则![]() ,则
,则![]() ,令
,令![]() ,因为
,因为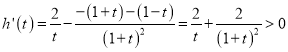 ,所以
,所以![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,所以
,所以![]() ,即
,即![]() .
.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目