题目内容
2.在△ABC中,AC=2AB=2,BC=$\sqrt{3}$,P是△ABC内部的一点,若∠APB=∠BPC=∠CPA,则PA+PB+PC=$\sqrt{7}$.分析 由∠APB=∠BPC=∠CPA=120°,∠ACB=60°,可以得到∠ACP=∠PBC,判定两个三角形相似,然后用相似三角形的性质计算求出PB、PC的长,再利用余弦定理求出PA,即可得出结论.
解答 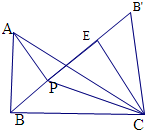 解:延长BP到B′,在BB'上取点E,使PE=PC,EB′=AP,
解:延长BP到B′,在BB'上取点E,使PE=PC,EB′=AP,
∵∠BPC=120°,
∴∠EPC=60°,
∴△PCE是正三角形,
∴∠CEB'=120°=∠APC
∵AP=EB′,PC=EC,
∴PC=CE,
∴△ACP≌△B′CE,
∴∠PCA=∠B′CE,AC=B′C=2
∴∠PCA+∠ACE=∠ACE+∠ECP
∴∠ACB′=∠PCE=60°,
∵AC=2AB=2,BC=$\sqrt{3}$,
∴AC2=BC2+AB2,
∴∠ABC=90°,∠ACB=30°
∴∠BCB′=90°,
∵PE=PC,AP=B′E
∴PA+PB+PC=PA+EP+B′E=BB′=$\sqrt{B{C}^{2}+BB{′}^{2}}$=$\sqrt{7}$,
故答案为:$\sqrt{7}$.
点评 本题考查的是相似三角形的判定与性质,考查余弦定理,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
14.已知ξ服从正态分布N(1,σ2),a∈R,则“P(ξ>a)=0.5”是“关于x的二项式${({ax+\frac{1}{x^2}})^3}$的展开式的常数项为3”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 既不充分又不必要条件 | D. | 充要条件 |
11.已知α∈(π,$\frac{3}{2}$π),cosα=-$\frac{4}{5}$,则tanα=( )
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | -$\frac{4}{3}$ | D. | -$\frac{3}{4}$ |