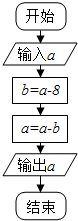
题目内容
15．计算：（1-$\frac{1}{{2}^{2}}$）（1-$\frac{1}{{3}^{2}}$）（1-$\frac{1}{{4}^{2}}$）…（1-$\frac{1}{201{1}^{2}}$）（1-$\frac{1}{201{2}^{2}}$）．分析 利用已知条件化简表达式，求解即可．
解答 解：（1-$\frac{1}{{2}^{2}}$）（1-$\frac{1}{{3}^{2}}$）（1-$\frac{1}{{4}^{2}}$）…（1-$\frac{1}{201{1}^{2}}$）（1-$\frac{1}{201{2}^{2}}$）
=$\frac{1×3×2×4×3×5×…×2011×2013}{{2}^{2}×{3}^{2}×{4}^{2}×…×{2012}^{2}}$
=$\frac{1×2013}{2×2012}$
=$\frac{2013}{4024}$．
点评 本题考查表达式求值，注意平方差公式的应用，考查计算能力．
练习册系列答案
阅读快车系列答案
相关题目
10．某程序框图如图所示，若其输出结果是56，则判断框中应填写的是（ ）
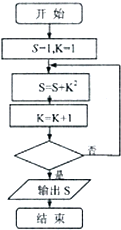
| A． | K＜4 | B． | K＜5 | C． | K＜6 | D． | K＜7 |
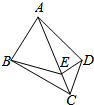如图，空间四边形ABCD，∠CAD=45°，cos∠ACB=$\frac{\sqrt{15}}{5}$，AC=$\sqrt{15}$+$\sqrt{10}$，AD=2$\sqrt{5}$，BC=6，若点E在线段AC上运动，则EB+ED的最小值为7．