题目内容
7.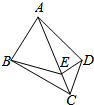 如图,空间四边形ABCD,∠CAD=45°,cos∠ACB=$\frac{\sqrt{15}}{5}$,AC=$\sqrt{15}$+$\sqrt{10}$,AD=2$\sqrt{5}$,BC=6,若点E在线段AC上运动,则EB+ED的最小值为7.
如图,空间四边形ABCD,∠CAD=45°,cos∠ACB=$\frac{\sqrt{15}}{5}$,AC=$\sqrt{15}$+$\sqrt{10}$,AD=2$\sqrt{5}$,BC=6,若点E在线段AC上运动,则EB+ED的最小值为7.
分析 在△ACD中,由已知结合余弦定理和正弦定理求得CD,cos∠ACD的值,然后展开多面体,在△BCD中利用余弦定理求解.
解答 解:在△ACD中,由AC=$\sqrt{15}$+$\sqrt{10}$,AD=2$\sqrt{5}$,∠CAD=45°,
利用余弦定理得:$C{D}^{2}=(\sqrt{15}+\sqrt{10})^{2}+(2\sqrt{5})^{2}-2×2\sqrt{5}$×$(\sqrt{15}+\sqrt{10})cos45°$=25,∴CD=5.
再由正弦定理得:$\frac{5}{\frac{\sqrt{2}}{2}}=\frac{2\sqrt{5}}{sinC}$,即sin∠ACD=$\frac{\sqrt{10}}{5}$,求得cos∠ACD=$\frac{\sqrt{15}}{5}$.
展开多面体如图:
EB+ED的最小值为BD,
在△BCD中,BC=6,CD=5,
∵cos∠ACB=$\frac{\sqrt{15}}{5}$,cos∠ACD=$\frac{\sqrt{15}}{5}$.
∴cos∠BCD=$2×(\frac{\sqrt{15}}{5})^{2}-1=\frac{1}{5}$.
∴BD=$\sqrt{{6}^{2}+{5}^{2}-2×6×5×\frac{1}{5}}=7$.
∴EB+ED的最小值为7.
故答案为:7.
点评 本题考查多面体表面上的最短距离问题,该类问题的解法是:首先剪展,然后在三角形中借助于正弦定理或余弦定理求解,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目