题目内容
9.已知△ABC是边长为1的正三角形,M、N分别是边AB、AC上的点,线段MN经过△ABC的中心G.若△AGM的面积为$\frac{1}{12}$,则△AGN的面积为$\frac{{\sqrt{3}+1}}{24}$.分析 设∠AGM=α,由已知可得AG,∠MAG的值,由正弦定理可得得GM=$\frac{\sqrt{3}}{6sin(α+\frac{π}{6})}$,由SAGM=$\frac{1}{2}$GM•GA•sinα=$\frac{1}{6(\sqrt{3}+cotα)}$=$\frac{1}{12}$,解得:cotα=2-$\sqrt{3}$,又利用正弦定理可得GN=$\frac{\sqrt{3}}{6sin(α-\frac{π}{6})}$,则可求SAGN=$\frac{1}{2}$GN•GA•sin(π-α)=$\frac{1}{6(\sqrt{3}-cotα)}$的值.
解答  解:因为G为边长为1的正三角形ABC的中心,
解:因为G为边长为1的正三角形ABC的中心,
所以AG=$\frac{2}{3}×\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{3}$,∠MAG=$\frac{π}{6}$,
由正弦定理$\frac{GM}{sin\frac{π}{6}}=\frac{GA}{sin(π-α-\frac{π}{6})}$,得GM=$\frac{\sqrt{3}}{6sin(α+\frac{π}{6})}$,.
则SAGM=$\frac{1}{2}$GM•GA•sinα=$\frac{sinα}{12sin(α+\frac{π}{6})}$=$\frac{1}{6(\sqrt{3}+cotα)}$)=$\frac{1}{12}$,
解得:cotα=2-$\sqrt{3}$,
又$\frac{GN}{sin\frac{π}{6}}=\frac{GA}{sin(α-\frac{π}{6})}$,得GN=$\frac{\sqrt{3}}{6sin(α-\frac{π}{6})}$,
则SAGN=$\frac{1}{2}$GN•GA•sin(π-α)=$\frac{sinα}{12sin(α-\frac{π}{6})}$=$\frac{1}{6(\sqrt{3}-cotα)}$=$\frac{1}{6(\sqrt{3}-2+\sqrt{3})}$=$\frac{{\sqrt{3}+1}}{24}$.
故答案为:$\frac{{\sqrt{3}+1}}{24}$
点评 本题主要考查了正弦定理,三角形面积公式的综合应用,将△AGM、△AGN的面积表示为α的函数是解题的关键.

| A. | $\frac{23}{90}$ | B. | $\frac{99}{23}$ | C. | $\frac{8}{15}$ | D. | $\frac{7}{30}$ |
| A. | 360 | B. | 180 | C. | 90 | D. | 45 |
| A. | (0,$\sqrt{2}$] | B. | [$\frac{\sqrt{2}}{2},\sqrt{2}$] | C. | ($\sqrt{2},2$) | D. | (1,$\sqrt{2}$] |
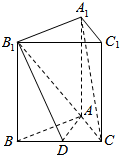 如图,已知三棱柱ABC-A1B1C1中,底面ABC是等腰直角三角形,侧棱AA1⊥底面ABC,D是BC的中点,AA1=AB=AC=2,
如图,已知三棱柱ABC-A1B1C1中,底面ABC是等腰直角三角形,侧棱AA1⊥底面ABC,D是BC的中点,AA1=AB=AC=2,