题目内容
19．在△ABC中，若∠C=90°，角A，B，C的对边分别为a，b，c，则$\frac{a+b}{c}$的取值范围是（ ）| A． | （0，$\sqrt{2}$] | B． | [$\frac{\sqrt{2}}{2}，\sqrt{2}$] | C． | （$\sqrt{2}，2$） | D． | （1，$\sqrt{2}$] |
分析 根据正弦定理进行化简，结合两角和差的正弦公式进行化简即可．
解答 解：由正弦定理得a=csinA，b=ccosA，
则$\frac{a+b}{c}$=sinA+cosA=$\sqrt{2}$sin（A+$\frac{π}{4}$），
∵0＜A＜$\frac{π}{2}$，
∴$\frac{π}{4}$＜A+$\frac{π}{4}$＜$\frac{3π}{4}$，
∴1＜$\sqrt{2}$sin（A+$\frac{π}{4}$≤$\sqrt{2}$，
即$\frac{a+b}{c}$的取值范围是（1，$\sqrt{2}$]，
故选：D．
点评 本题主要考查正弦定理的应用，利用两角和差的正弦公式以及三角函数的性质是解决本题的关键．
练习册系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
7．设函数f（x）=$\frac{x}{sinx}$，则f′（$\frac{π}{2}$）等于（ ）
| A． | -$\frac{π}{2}$ | B． | $\frac{π}{2}$ | C． | 1 | D． | -1 |
14．某大型企业人力资源部为研究企业员工工作积极性和对待企业改革态度的关系，随机抽取了180名员工进行调查，所得数据如下表所示：
对于人力资源部的研究项目，根据上述数据盘算能否在犯错误的概率不超过0.5%的情况下认为工作积极和支持企业改革有关系．
附：公式及相关数据：
k2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$（其中n=a+b+c+d）．
| 积极支持企业改革 | 不太赞成企业改革 | 总计 | |
| 工作积极 | 50 | 40 | 90 |
| 工作不积极 | 30 | 60 | 90 |
| 总计 | 80 | 100 | 180 |
附：公式及相关数据：
| P（k2≥k0） | 0.50 | 0.05 | 0.005 |
| k0 | 0.455 | 3.841 | 10.828 |
4．某区高一年级的一次数学统考中，随机抽取M名同学的成绩，数据的分组统计表如下：
（1）求出表中m，n，M，N的值；
（2）若该区高一学生有5000人，试估计这次统考中该区高一学生的平均分数及分数在区间（60，90]内的人数．
| 分组 | 频数 | 频率 |
| （40，50] | 2 | 0.02 |
| （50.60] | 4 | 0.04 |
| （60，70] | 11 | 0.11 |
| （70，80] | 38 | 0.38 |
| （80，90] | m | n |
| （90，100] | 11 | 0.11 |
| 合计 | M | N |
（2）若该区高一学生有5000人，试估计这次统考中该区高一学生的平均分数及分数在区间（60，90]内的人数．
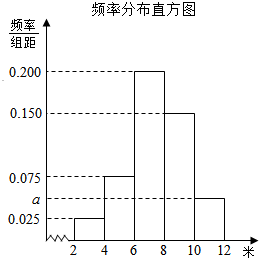为了解某市今年初二年级男生的身体素质状况，从该市初二年级男生中抽取了一部分学生进行“掷实心球”的项目测试．成绩低于6米为不合格，成绩在6至8米（含6米不含8米）的为及格，成绩在8米至12米（含8米和12米，假定该市初二学生掷实心球均不超过12米）为优秀．把获得的所有数据，分成[2，4），[4，6），[6，8），[8，10），[10，12]五组，画出的频率分布直方图如图所示．已知有4名学生的成绩在10米到12米之间．