题目内容
1.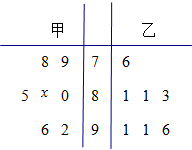 某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85.
某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85.(Ⅰ) 计算甲班7位学生成绩的方差s2;
(Ⅱ)从成绩在90分以上的学生中随机抽取两名学生,求甲班至少有一名学生的概率.
参考公式:
方差${s^2}=\frac{1}{n}[{{{({{x_1}-\overline x})}^2}+{{({{x_2}-\overline x})}^2}+…+{{({{x_n}-\overline x})}^2}}]$,其中$\overline x=\frac{{{x_1}+{x_2}+…+{x_n}}}{n}$.
分析 (Ⅰ)利用平均数求出x的值,根据所给的茎叶图,得出甲班7位学生成绩,做出这7次成绩的平均数,把7次成绩和平均数代入方差的计算公式,求出这组数据的方差.
(Ⅱ)设甲班至少有一名学生为事件A,其对立事件为从成绩在90分以上的学生中随机抽取两名学生,甲班没有一名学生;先计算出从成绩在90分以上的学生中随机抽取两名学生的所有抽取方法总数,和没有甲班一名学生的方法数目,先求出从成绩在90分以上的学生中随机抽取两名学生,甲班没有一名学生的概率,进而结合对立事件的概率性质求得答案
解答 解:( I)∵甲班学生的平均分是85,
∴$\frac{92+96+80+80+x+85+79+78}{7}=85$.…(1分)
∴x=5.…(3分)
则甲班7位学生成绩的方差为s2=$\frac{1}{7}[{{{({-6})}^2}+{{({-7})}^2}+{{({-5})}^2}+{0^2}+{0^2}+{7^2}+{{11}^2}}]$=40.…(6分)
( II)甲班成绩在90(分)以上的学生有两名,分别记为A,B,…(7分)
乙班成绩在90(分)以上的学生有三名,分别记为C,D,E. …(8分)
从这五名学生任意抽取两名学生共有10种情况:(A,B),(A,C),(A,D),(A,E),(B,C),(B,D),(B,E),(C,D),(C,E),(D,E). …(9分)
其中甲班至少有一名学生共有7种情况:(A,B),(A,C),(A,D),(A,E),(B,C),(B,D),(B,E).…(10分)
记“甲班至少有一名学生”为事件M,则$P(M)=\frac{7}{10}$,
即从成绩在90(分)以上的学生中随机抽取两名学生,甲校至少有一名学生的概率为$\frac{7}{10}$. …(12分)
点评 本小题主要考查茎叶图、样本均值、样本方差、概率等知识,考查或然与必然的数学思想方法,以及数据处理能力、运算求解能力和应用意识.

| A. | $\frac{5}{12}$ | B. | $\frac{1}{2}$ | C. | $\frac{7}{12}$ | D. | $\frac{5}{6}$ |

| A. | 函数f(x)在x=x1处取得极小值 | B. | 函数f(x)在x=x3处取得极大值 | ||
| C. | 函数f(x)的单调递减区间是(x2,x3) | D. | 函数f(x)无极大值 |
 从4种不同的颜色中选择若干种给如图所示的4个方格涂色,每个方格中只涂一种颜色且相邻两格不能涂同一种颜色,则不同的涂色方法共有( )
从4种不同的颜色中选择若干种给如图所示的4个方格涂色,每个方格中只涂一种颜色且相邻两格不能涂同一种颜色,则不同的涂色方法共有( )| A. | 24种 | B. | 72种 | C. | 96种 | D. | 108种 |