设函数f(x)=x3-3x2-9x.求函数f(x)的极大值．题目和参考答案——青夏教育精英家教网——

题目内容

9．设函数f（x）=x³-3x²-9x，求函数f（x）的极大值．

分析先求出函数的导数，得到函数的单调区间，从而求出函数的极大值．

解答解：f′（x）=3x²-6x-9=3（x-3）（x+1），
令f′（x）＞0，解得：x＞3或x＜-1，
令f′（x）＜0，解得：-1＜x＜3，
∴函数f（x）在（-∞，-1），（3，+∞）递增，在（-1，3）递减，
∴f（x）_极大值=f（-1）=-1-3+9=5．

点评本题考查了函数的单调性，函数的极值问题，考查导数的应用，是一道基础题．

练习册系列答案

夺冠金卷单元同步测试系列答案

夺冠课时导学案系列答案

发现会考系列答案

发展性评价系列答案

仿真试卷系列答案

非常好冲刺系列答案

非考不可年级衔接总复习系列答案

分层学习检测与评价系列答案

普通高中招生考试命题指导纲要系列答案

高分计划系列答案

相关题目

19．有A、B、C、D、E共5人并排站一起，若A、B必须相邻，且B在A的右边，那么不同的站法有（　　）

20．已知点A（7，-4），B（-5，6）则线段AB垂直平分线方程是（　　）

17．化简2$\sqrt{1+sin10}$+$\sqrt{2+2cos10}$的结果是（　　）

4．下列六个关系式：①{a，b}⊆{b，a}；②{a，b}={b，a}；③{0}=∅；④0∈{0}；⑤∅∈{0}；⑥∅⊆{0}，其中正确的个数为（　　）

14．设F₁，F₂是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$的两个焦点，P在双曲线上，若$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=0$，$|{\overrightarrow{P{F_1}}}|•|{\overrightarrow{P{F_2}}}|=2ac$（c为半焦距），则双曲线的离心率为（　　）

$\frac{{\sqrt{3}-1}}{2}$

$\frac{{\sqrt{3}+1}}{2}$

$\frac{{\sqrt{5}+1}}{2}$

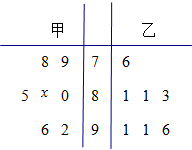某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛，他们取得的成绩（满分100分）的茎叶图如图，其中甲班学生的平均分是85．
（Ⅰ）计算甲班7位学生成绩的方差s²；
（Ⅱ）从成绩在90分以上的学生中随机抽取两名学生，求甲班至少有一名学生的概率．
参考公式：
方差${s^2}=\frac{1}{n}[{{{（{{x_1}-\overline x}）}^2}+{{（{{x_2}-\overline x}）}^2}+…+{{（{{x_n}-\overline x}）}^2}}]$，其中$\overline x=\frac{{{x_1}+{x_2}+…+{x_n}}}{n}$．

18．已知函数f（x）=tanx-sinx，下列命题中正确的是②③（写出所有正确命题的序号）
①f（x）的周期为π； ②f（x）的图象关于点（π，0）对称；
③f（x）在（$\frac{π}{2}，π$）上单调递增； ④f（x）在（-$\frac{π}{2}$，$\frac{π}{2}$）上有3个零点．

15．已知α是第二象限的角，且$sinα=\frac{3}{5}$，则tan2α的值是-$\frac{24}{7}$．