题目内容
6.函数y=f(x)的导函数y=f′(x)的图象如图所示,下列说法正确的是( )
| A. | 函数f(x)在x=x1处取得极小值 | B. | 函数f(x)在x=x3处取得极大值 | ||
| C. | 函数f(x)的单调递减区间是(x2,x3) | D. | 函数f(x)无极大值 |
分析 直接利用导函数的图象的值域,判断函数的单调性即可.
解答 解:函数f(x)的导函数f′(x)的图象如图所示,
可得x∈(-∞,x2),(x3,+∞),f′(x)>0,所以函数f(x)是增函数.x∈(x2,x3),f′(x)<0,函数是减函数.
函数f(x)在x=x2时取极大值,在x=x3,函数取得极小值,
所以选项C正确.
故选:C.
点评 本题考查函数的导数以及函数的图象的应用,考查基本知识的应用.

练习册系列答案
相关题目
16.在等差数列{an}中,a1+a19=10,则a10的值为( )
| A. | 5 | B. | 6 | C. | 8 | D. | 10 |
17.化简2$\sqrt{1+sin10}$+$\sqrt{2+2cos10}$的结果是( )
| A. | 2sin5 | B. | 4cos5+2sin5 | C. | -4cos5-2sin5 | D. | -2sin5 |
14.设F1,F2是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的两个焦点,P在双曲线上,若$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=0$,$|{\overrightarrow{P{F_1}}}|•|{\overrightarrow{P{F_2}}}|=2ac$(c为半焦距),则双曲线的离心率为( )
| A. | $\frac{{\sqrt{3}-1}}{2}$ | B. | $\frac{{\sqrt{3}+1}}{2}$ | C. | 2 | D. | $\frac{{\sqrt{5}+1}}{2}$ |
15.已知x,y的取值如表所示:若y与x呈线性相关,且回归方程为$\widehat{y}$=$\widehat{b}$x+$\frac{7}{2}$,则$\widehat{b}$等于0.5
| x | 2 | 3 | 4 |
| y | 5 | 4 | 6 |
12.如图所示的算法流程图运行后,输出结果是( )
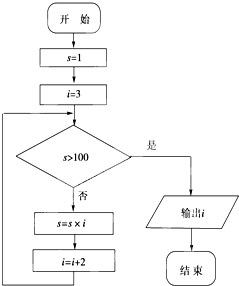

| A. | 7 | B. | 8 | C. | 9 | D. | 11 |
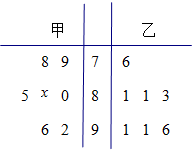 某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85.
某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85.