题目内容
11.解关于x的不等式:解关于x的不等式:x2+2a≥2ax+x.分析 把不等式化为(x-1)(x-2a)≥0,讨论a的取值,求出对应不等式的解集.
解答 解:不等式:x2+2a≥2ax+x可化为(x-1)(x-2a)≥0,
对应方程(x-1)(x-2a)=0的两根为x1=1,x2=2a;
①当2a>1,即a>$\frac{1}{2}$时,解得x<1或x>2a;
②当2a<1,即a<$\frac{1}{2}$时,解得x<2a或x>1;
③当2a=1,即a=$\frac{1}{2}$时,解得x∈R;
综上:当a>$\frac{1}{2}$时,不等式的解集为(-∞,1)∪(2a,+∞),
当a=$\frac{1}{2}$时,不等式的解集为R,
当a<$\frac{1}{2}$时,不等式的解集为(-∞,2a)(1,+∞).
点评 本题考查了含有字母系数的不等式的解法与应用问题,解题时应对字母系数进行讨论,是基础题目.

练习册系列答案
相关题目
2.已知cos(π-α)=-$\frac{5}{13}$且α是第四象限角,则sinα=( )
| A. | $\frac{5}{13}$ | B. | $\frac{12}{13}$ | C. | ±$\frac{12}{13}$ | D. | -$\frac{12}{13}$ |
19.有A、B、C、D、E共5人并排站一起,若A、B必须相邻,且B在A的右边,那么不同的站法有( )
| A. | 24种 | B. | 36种 | C. | 48种 | D. | 60种 |
6.在△ABC中,已知A是三角形的内角,且sinA+cosA=$\frac{3}{5}$,则△ABC一定是( )
| A. | 锐角三角形 | B. | 直角三角形 | ||
| C. | 钝角三角形 | D. | 无法确定三角形的形状 |
16.在等差数列{an}中,a1+a19=10,则a10的值为( )
| A. | 5 | B. | 6 | C. | 8 | D. | 10 |
3.已知平面上的动点C(x,y)与两个定点A(26,1),B(2,1)满足|$\overrightarrow{AC}$|=5|$\overrightarrow{BC}$|,则△ABC的面积的最大值为( )
| A. | 12 | B. | 24 | C. | 60 | D. | 以上答案都不对 |
20.已知点A(7,-4),B(-5,6)则线段AB垂直平分线方程是( )
| A. | 6x-5y-1=0 | B. | 5x+6y+1=0 | C. | 6x+5y-1=0 | D. | 5x-6y-1=0 |
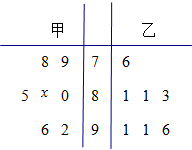 某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85.
某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85.