题目内容
12.掷两次骰子得到的点数分别为m和n,记向量$\overrightarrow{a}$=(m,n)与向量$\overrightarrow{b}$=(1,-1)的夹角为θ,则θ∈(0,$\frac{π}{2}$]的概率是( )| A. | $\frac{5}{12}$ | B. | $\frac{1}{2}$ | C. | $\frac{7}{12}$ | D. | $\frac{5}{6}$ |
分析 由已知掷两次骰子得到的点数分别为m和n,记为(m,n),共有36种可能,而由数量积则θ∈(0,$\frac{π}{2}$]的,n范围是m-n≥0并且m+n≠0,由几何概型公式得到所求.
解答 解:解:连掷两次骰子得到的点数分别为m和n,记(m,n)有:
(1,1),(1,2),(1,3),(1,4),(1,5),(1,6)
(2,1),(2,2),(2,3),(2,4),(2,5),(2,6)
(3,1),(3,2),(3,3),(3,4),(3,5),(3,6)
(4,1),(4,2),(4,3),(4,4),(4,5),(4,6)
(5,1),(5,2),(5,3),(5,4),(5,5),(5,6)
(6,1),(6,2),(6,3),(6,4),(6,5),(6,6),共36个基本事件
若θ∈(0,$\frac{π}{2}$],则m≥n,则满足条件的(m,n)有:
(1,1),(2,1),(2,2),(3,1),(3,2),(3,3)
(4,1),(4,2),(4,3),(4,4),(5,1),(5,2)
(5,3),(5,4),(5,5),(6,1),(6,2),(6,3)
(6,4),(6,5),(6,6),共21个基本事件
则P=$\frac{21}{36}=\frac{7}{12}$;
故选C.
点评 本题主要考查古典概型概率求法,用到了用两个向量的数量积表示两个向量的夹角;解答本题的关键是明确概率模型,分别求出所有事件以及满足条件的事件个数,利用公式解答.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
2.已知cos(π-α)=-$\frac{5}{13}$且α是第四象限角,则sinα=( )
| A. | $\frac{5}{13}$ | B. | $\frac{12}{13}$ | C. | ±$\frac{12}{13}$ | D. | -$\frac{12}{13}$ |
3.已知平面上的动点C(x,y)与两个定点A(26,1),B(2,1)满足|$\overrightarrow{AC}$|=5|$\overrightarrow{BC}$|,则△ABC的面积的最大值为( )
| A. | 12 | B. | 24 | C. | 60 | D. | 以上答案都不对 |
20.已知点A(7,-4),B(-5,6)则线段AB垂直平分线方程是( )
| A. | 6x-5y-1=0 | B. | 5x+6y+1=0 | C. | 6x+5y-1=0 | D. | 5x-6y-1=0 |
7.Sn是等差数列{an}的前n项和,若a2+a4+a15是一个确定的常数,则在数列{Sn}中也是确定常数的项是( )
| A. | S7 | B. | S4 | C. | S13 | D. | S16 |
17.化简2$\sqrt{1+sin10}$+$\sqrt{2+2cos10}$的结果是( )
| A. | 2sin5 | B. | 4cos5+2sin5 | C. | -4cos5-2sin5 | D. | -2sin5 |
2.已知平面α,β和直线a,b,若α∩β=l,a?α,b?β,且平面与平面β不垂直,直线a与直线l不垂直,直线b与直线l不垂直,则( )
| A. | 直线a与直线b可能垂直,但不可能平行 | |
| B. | 直线a与直线b可能垂直,也可能平行 | |
| C. | 直线a与直线b不可能垂直,但可能平行 | |
| D. | 直线a与直线b不可能垂直,也不可能平行 |
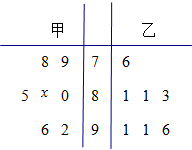 某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85.
某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85.