题目内容
13.以坐标原点为顶点,(-1,0)为焦点的抛物线的方程为y2=-4x.分析 由焦点(-1,0),可设抛物线的方程为y2=-2px,由$\frac{p}{2}$=1可求p,即可求出抛物线的方程.
解答 解:由焦点(-1,0),可设抛物线的方程为y2=-2px
∵$\frac{p}{2}$=1
∴p=2
∴y2=-4x.
故答案为:y2=-4x.
点评 本题主要考查了由抛物线的性质求解抛物线的方程,解题的关键是由抛物线的焦点确定抛物线的开口方向,属于基础试题.

练习册系列答案
相关题目
3.已知平面上的动点C(x,y)与两个定点A(26,1),B(2,1)满足|$\overrightarrow{AC}$|=5|$\overrightarrow{BC}$|,则△ABC的面积的最大值为( )
| A. | 12 | B. | 24 | C. | 60 | D. | 以上答案都不对 |
5.二项式${({x+\frac{1}{x}})^4}$的展开式中的常数项是( )
| A. | 1 | B. | 2 | C. | 6 | D. | 12 |
2.已知平面α,β和直线a,b,若α∩β=l,a?α,b?β,且平面与平面β不垂直,直线a与直线l不垂直,直线b与直线l不垂直,则( )
| A. | 直线a与直线b可能垂直,但不可能平行 | |
| B. | 直线a与直线b可能垂直,也可能平行 | |
| C. | 直线a与直线b不可能垂直,但可能平行 | |
| D. | 直线a与直线b不可能垂直,也不可能平行 |
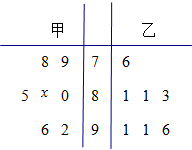 某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85.
某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85.