题目内容
7. 从4种不同的颜色中选择若干种给如图所示的4个方格涂色,每个方格中只涂一种颜色且相邻两格不能涂同一种颜色,则不同的涂色方法共有( )
从4种不同的颜色中选择若干种给如图所示的4个方格涂色,每个方格中只涂一种颜色且相邻两格不能涂同一种颜色,则不同的涂色方法共有( )| A. | 24种 | B. | 72种 | C. | 96种 | D. | 108种 |
分析 分类讨论,利用排列知识,即可得出结论.
解答 解:用两种颜色时,涂法有2${C}_{4}^{2}$种;用三种颜色时,涂法有3${C}_{4}^{3}$${C}_{3}^{1}$${C}_{2}^{1}$种;用四种颜色时,涂法有${A}_{4}^{4}$种,
所以不同的涂色方法共有12+72+24=108种,
另解:4×3×3×3=108种.
故选:D.
点评 本题考查排列知识,考查分类讨论的数学思想,比较基础.

练习册系列答案
相关题目
2.已知平面α,β和直线a,b,若α∩β=l,a?α,b?β,且平面与平面β不垂直,直线a与直线l不垂直,直线b与直线l不垂直,则( )
| A. | 直线a与直线b可能垂直,但不可能平行 | |
| B. | 直线a与直线b可能垂直,也可能平行 | |
| C. | 直线a与直线b不可能垂直,但可能平行 | |
| D. | 直线a与直线b不可能垂直,也不可能平行 |
2.为了得到函数y=tan(2x-$\frac{π}{6}$)的图象,可以将函数y=tan2x的图象( )
| A. | 向右平移$\frac{π}{6}$个单位长度 | B. | 向右平移$\frac{π}{12}$个单位长度 | ||
| C. | 向左平移$\frac{π}{6}$个单位长度 | D. | 向左平移$\frac{π}{12}$个单位长度 |
12.如图所示的算法流程图运行后,输出结果是( )
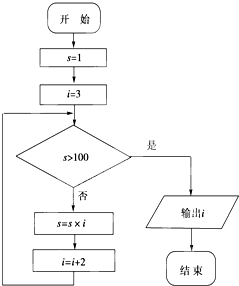

| A. | 7 | B. | 8 | C. | 9 | D. | 11 |
16.若平面α的一个法向量$\overrightarrow n$=(2,1,1),直线l的一个方向向量为$\overrightarrow a$=(1,2,3),则l与α所成角的正弦值为( )
| A. | $\frac{\sqrt{17}}{6}$ | B. | $\frac{\sqrt{21}}{6}$ | C. | -$\frac{\sqrt{21}}{6}$ | D. | $\frac{\sqrt{21}}{3}$ |
17.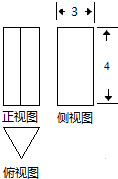 如图,一个几何体的三视图,侧视图和正视图均为矩形,俯视图为正三角形,尺寸如图,则该几何体的体积为( )
如图,一个几何体的三视图,侧视图和正视图均为矩形,俯视图为正三角形,尺寸如图,则该几何体的体积为( )
 如图,一个几何体的三视图,侧视图和正视图均为矩形,俯视图为正三角形,尺寸如图,则该几何体的体积为( )
如图,一个几何体的三视图,侧视图和正视图均为矩形,俯视图为正三角形,尺寸如图,则该几何体的体积为( )| A. | 18 | B. | 9$\sqrt{3}$ | C. | 12$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
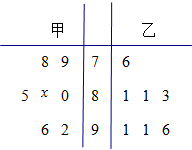 某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85.
某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85.