题目内容
16.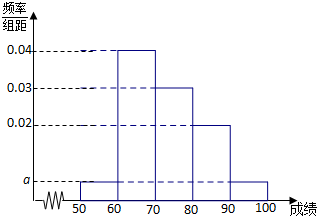 某校1000名学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
某校1000名学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].(1)求图中a的值;
(2)根据频率分布直方图,估计这1000名学生数学成绩的平均分;
(3)若这1000名学生数学成绩某些分数段的人数(x)与语文成绩相应分数段的人数(y)之比如表所示,求语文成绩在[50,90)之外的人数.
| 分数段 | [50,60) | [60,70) | [70,80) | [80,90) |
| x:y | 1:1 | 4:5 | 3:2 | 2:1 |
分析 (1)根据频率分布直方图所有小矩形的面积之和为1,求a.
(2)根据平均数公式计算即可,
(3)先求出语文成绩在[50,90)之内的人数,用1000减去此数,得出结果
解答 (1)由频率分布图可知:(2a+0.02+0.03+0.04)×10=1?a=0.005…(4分)
(2)由频率分布图可得该校1000名学生的数学成绩平均分为55×0.05+65×0.4+75×0.3+85×0.2+95×0.05=73…(8分)
(3)语文成绩在[50,90)内的人数为$({0•005+\frac{5}{4}×0•04+\frac{2}{3}×0•03+\frac{1}{2}×0•02})×10×1000=850$人
语文成绩在[50,90)外的人数为1000-850=150人 …1(2分)
点评 本题考查频率分布估计总体分布,解题的关键是理解频率分布直方图,熟练掌握频率分布直方图的性质,且能根据所给的数据建立恰当的方程求解.

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
11.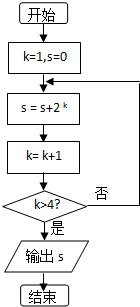 执行如图所示的程序框图,则输出s的值为( )
执行如图所示的程序框图,则输出s的值为( )
 执行如图所示的程序框图,则输出s的值为( )
执行如图所示的程序框图,则输出s的值为( )| A. | 30 | B. | 31 | C. | 62 | D. | 63 |