题目内容

6．已知3a=2，3b=$\frac{1}{5}$，则32a-b=20．

分析 对3a=2，3b=$\frac{1}{5}$两边取对数，求出a，b的值，再计算2a-b的值，再根据指数和对数的运算性质即可求出答案．

解答 解：∵3a=2，3b=$\frac{1}{5}$，
两边取对数得a=log32，b=log3$\frac{1}{5}$=-log35，
∴2a-b=2log32+log35=log320，
∴32a-b=20，
故答案为：20．

点评 本题考查了对数函数和指数函数的运算性质，属于基础题．

练习册系列答案
相关题目
1．已知数列{an}满足：an=an-1+1（n≥2，n∈N），且a3是a1与a5+2的等比中项．
（1）求数列{an}的通项公式an以及前n项和Sn；
（2）若${b_n}={2^{a_n}}$（n∈N*），求数列{bn}的前n项和 Tn．
2．椭圆C：$\frac{x^2}{16}+\frac{y^2}{9}$=1的左、右顶点分别为A1，A2，点P是C上异于顶点的任一点，则直线PA2与直线PA1的斜率之积是（　　）
A．-$\frac{3}{4}$B．-$\frac{9}{16}$C．-$\frac{4}{3}$D．-$\frac{16}{9}$
14．求适合下列条件的椭圆的标准方程：
（1）椭圆上一点P（3，2）到两焦点的距离之和为8；
（2）椭圆两焦点间的距离为16，且椭圆上某一点到两焦点的距离分别等于9或15．
1．函数y=$\frac{3{x}^{2}}{\sqrt{1-2x}}$+（2x+1）2的定义域为（　　）
A．{x|x＜$\frac{1}{2}$}B．{x|x＜$\frac{1}{2}$且x≠-$\frac{1}{2}$}C．{x|x＞$\frac{1}{2}$}D．{x|x≤$\frac{1}{2}$且x≠-$\frac{1}{2}$}
11．已知函数f（x）=$\frac{a-{2}^{x}}{1+{2}^{x}}$（a∈R），且x∈R时，总有f（-x）=-f（x）成立．
（1）求a的值；
（2）判断并证明函数f（x）的单调性；
（3）求f（x）在[0，2]上的值域．
18．设奇函数f（x）与g（x）偶函数的定义域都为（-∞，+∞），且满足f（x）+g（x）=2x，有下列命题：
①g（x）≥1在（-∞，+∞）恒成立；
②f（x）2-g（x）2=-1在（-∞，+∞）恒成立；
③f（x）≤g（x）在（-∞，+∞）恒成立；
④g（2x）=2f（x）g（x）在（-∞，+∞）恒成立．
则真命题是①②③（填所有真命题的序号）．
15．已知函数f（x）=$\frac{x}{{e}^{x}}$（x∈R），若x1≠x2，且f（x1）=f（x2），则x1，2-x2大小关系是（　　）
A．x1＞2-x2B．x1＜2-x2
C．x1=2-x2D．x1与2-x2大小不确定
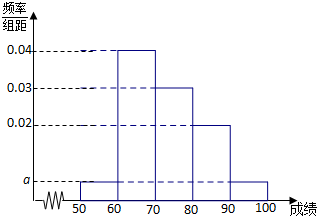16．某校1000名学生期中考试数学成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]．
（1）求图中a的值；
（2）根据频率分布直方图，估计这1000名学生数学成绩的平均分；
（3）若这1000名学生数学成绩某些分数段的人数（x）与语文成绩相应分数段的人数（y）之比如表所示，求语文成绩在[50，90）之外的人数．
分数段[50，60）[60，70）[70，80）[80，90）
x：y1：14：53：22：1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网