题目内容
4．已知动圆M与圆C1：（x+5）2+y2=16外切，与圆C2：（x-5）2+y2=16内切，则动圆圆心的轨迹方程为$\frac{x^2}{16}-\frac{y^2}{9}=1（x＞0）$．分析 设动圆圆心M（x，y），半径为r，则|MC1|=r+4，|MC2|=r-4，可得|MC1|-|MC2|=r+4-r+4=8＜|C1C2|=10，利用双曲线的定义，即可求动圆圆心M的轨迹方程．
解答 解：设动圆圆心M的坐标为（x，y），半径为r，则|MC1|=r+4，|MC2|=r-4，
∴|MC1|-|MC2|=r+4-r+4=8＜|C1C2|=10，
由双曲线的定义知，点M的轨迹是以C1、C2为焦点的双曲线的右支，且2a=8，a=4，b=3
双曲线的方程为：$\frac{{x}^{2}}{16}-\frac{{y}^{2}}{9}=1$（x＞0）．
点评 本题考查圆与圆的位置关系，考查双曲线的定义，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
15．已知函数f（x）=$\frac{x}{{e}^{x}}$（x∈R），若x1≠x2，且f（x1）=f（x2），则x1，2-x2大小关系是（ ）
| A． | x1＞2-x2 | B． | x1＜2-x2 | ||
| C． | x1=2-x2 | D． | x1与2-x2大小不确定 |
16．
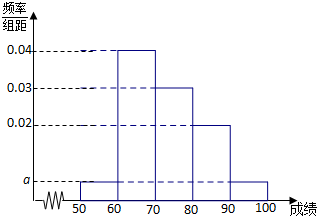某校1000名学生期中考试数学成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]．
（1）求图中a的值；
（2）根据频率分布直方图，估计这1000名学生数学成绩的平均分；
（3）若这1000名学生数学成绩某些分数段的人数（x）与语文成绩相应分数段的人数（y）之比如表所示，求语文成绩在[50，90）之外的人数．
某校1000名学生期中考试数学成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]．（1）求图中a的值；
（2）根据频率分布直方图，估计这1000名学生数学成绩的平均分；
（3）若这1000名学生数学成绩某些分数段的人数（x）与语文成绩相应分数段的人数（y）之比如表所示，求语文成绩在[50，90）之外的人数．
| 分数段 | [50，60） | [60，70） | [70，80） | [80，90） |
| x：y | 1：1 | 4：5 | 3：2 | 2：1 |
14．如果函数y=3sin（2x+ϕ）的图象关于点$（\frac{π}{3}，0）$中心对称，那么ϕ的一个值可以为（ ）
| A． | $\frac{π}{3}$ | B． | $-\frac{π}{3}$ | C． | $\frac{π}{6}$ | D． | $-\frac{π}{6}$ |