题目内容
8．已知sin（x-40°）=cos（x+10°）-cos（x-10°），则tanx=$\frac{\sqrt{3}}{3}$．分析 由和差角的公式变形已知式子可得tanx=$\frac{sin40°}{cos40°+2sin10°}$，再由和差角的公式化简即可．
解答 解：∵sin（x-40°）=cos（x+10°）-cos（x-10°），
∴sinxcos40°-cosxsin40°=cosxcos10°-sinxsin10°-cosxcos10°-sinxsin10°，
∴sinxcos40°-cosxsin40°=-2sinxsin10°，
∴（cos40°+2sin10°）sinx=cosxsin40°，
∴tanx=$\frac{sinx}{cosx}$=$\frac{sin40°}{cos40°+2sin10°}$=$\frac{sin40°}{cos（30°+10°）+2sin10°}$
=$\frac{sin40°}{\frac{\sqrt{3}}{2}cos10°-\frac{1}{2}sin10°+2sin10°}$=$\frac{sin40°}{\frac{\sqrt{3}}{2}cos10°+\frac{3}{2}sin10°}$
=$\frac{sin40°}{\sqrt{3}（\frac{1}{2}cos10°+\frac{\sqrt{3}}{2}sin10°）}$=$\frac{sin40°}{\sqrt{3}sin（30°+10°）}$=$\frac{\sqrt{3}}{3}$
故答案为：$\frac{{\sqrt{3}}}{3}$
点评 本题考查和差角的三角函数公式，熟练应用公式是解决问题的关键，属中档题．
练习册系列答案
阅读快车系列答案
相关题目
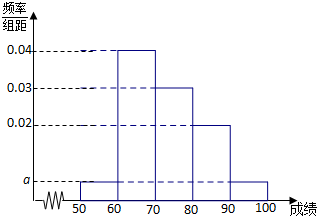某校1000名学生期中考试数学成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]．