题目内容
6．曲线y=$\frac{1}{3}{x^3}+2{x^2}$-ax-1上横坐标为2的点处的切线平行于x轴，那么a=（ ）| A． | 4 | B． | 12 | C． | 6 | D． | 16 |
分析 求出原函数的导函数，得到函数在x=2时的导数值，由导数值等于0求得a的值．
解答 解：由y=$\frac{1}{3}{x^3}+2{x^2}$-ax-1，得：y′=x2+4x-a，
∴y′|x=2=12-a．
∵曲线y=$\frac{1}{3}{x^3}+2{x^2}$-ax-1上横坐标为2的点处的切线平行于x轴，
∴12-a=0，即a=12．
故选：B．
点评 本题考查利用导数研究曲线上某点处的切线方程，过曲线上某点的切线的斜率，就是函数在该点处的导数值，是中档题．
练习册系列答案
相关题目
16．
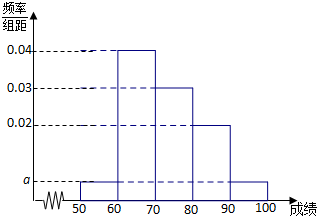某校1000名学生期中考试数学成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]．
（1）求图中a的值；
（2）根据频率分布直方图，估计这1000名学生数学成绩的平均分；
（3）若这1000名学生数学成绩某些分数段的人数（x）与语文成绩相应分数段的人数（y）之比如表所示，求语文成绩在[50，90）之外的人数．
某校1000名学生期中考试数学成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]．（1）求图中a的值；
（2）根据频率分布直方图，估计这1000名学生数学成绩的平均分；
（3）若这1000名学生数学成绩某些分数段的人数（x）与语文成绩相应分数段的人数（y）之比如表所示，求语文成绩在[50，90）之外的人数．
| 分数段 | [50，60） | [60，70） | [70，80） | [80，90） |
| x：y | 1：1 | 4：5 | 3：2 | 2：1 |
14．如果函数y=3sin（2x+ϕ）的图象关于点$（\frac{π}{3}，0）$中心对称，那么ϕ的一个值可以为（ ）
| A． | $\frac{π}{3}$ | B． | $-\frac{π}{3}$ | C． | $\frac{π}{6}$ | D． | $-\frac{π}{6}$ |
11．函数f（x）=3sin（x+10°）+5sin（x+70°）的最大值是（ ）
| A． | 7 | B． | $\sqrt{34}$ | C． | 4 | D． | 8 |