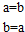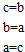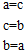题目内容
1.已知命题P:若幂函数f(x)=xα过点(2,8),实数a满足f(2-a)>f(a-1).命题Q:实数a满足2a-1>1.且P∧Q为真,求实数a的取值范围.分析 2α=8⇒α=3,则f(x)=x3.若P真:f(2-a)>f(a-1),利用函数f(x)的单调性可得a范围;若Q真:2a-1>1,利用指数函数的单调性可得a-1>0,解得a范围.由P∧Q为真,求其交集即可.
解答 解:∵2α=8⇒α=3,则f(x)=x3,
若P真:f(2-a)>f(a-1),$⇒2-a>a-1⇒a<\frac{3}{2}$;
若Q真:2a-1>1,∴a-1>0,解得a>1.
∵P∧Q为真,
∴$\left\{{\begin{array}{l}{a<\frac{3}{2}}\\{a>1}\end{array}}\right.⇒1<a<\frac{3}{2}$.
∴实数a的取值范围是$(1,\frac{3}{2})$.
点评 本题考查了复合命题真假的判定、函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
16.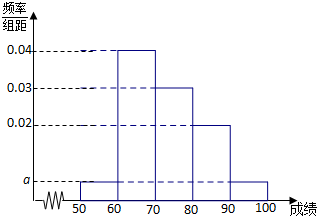 某校1000名学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
某校1000名学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
(1)求图中a的值;
(2)根据频率分布直方图,估计这1000名学生数学成绩的平均分;
(3)若这1000名学生数学成绩某些分数段的人数(x)与语文成绩相应分数段的人数(y)之比如表所示,求语文成绩在[50,90)之外的人数.
 某校1000名学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
某校1000名学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].(1)求图中a的值;
(2)根据频率分布直方图,估计这1000名学生数学成绩的平均分;
(3)若这1000名学生数学成绩某些分数段的人数(x)与语文成绩相应分数段的人数(y)之比如表所示,求语文成绩在[50,90)之外的人数.
| 分数段 | [50,60) | [60,70) | [70,80) | [80,90) |
| x:y | 1:1 | 4:5 | 3:2 | 2:1 |
11.函数f(x)=3sin(x+10°)+5sin(x+70°)的最大值是( )
| A. | 7 | B. | $\sqrt{34}$ | C. | 4 | D. | 8 |