题目内容
已知在等比数列{an}中,2a2=a1+a3-1,a1=1.
(1)若数列{bn}满足b1+
+
+…+
=an(n∈N*),求数列{bn}的通项公式;
(2)求数列{bn}的前n项和Sn.
(1)若数列{bn}满足b1+
| b2 |
| 2 |
| b3 |
| 3 |
| bn |
| n |
(2)求数列{bn}的前n项和Sn.
(1)设数列{an}的公比为q,2a2=a1+a3-1,
即2a1q=a1+a1q2-1,
∵a1=1,∴2q=q2,
∵q≠0,∴q=2,an=2n-1.
又b1+
+
+…+
=an,①
当n≥2时,b1+
+
+…+
=an-1,②
①-②,得
=an-an-1=2n-1-2n-2=2n-2,
∴bn=n•2n-2,n≥2.
∴bn=
.
(2)由(1)得Sn=1+2×20+3×21+4×22+…+n•2n-2,③
2Sn=2+2×21+3×22+…+(n-1)•2n-2+n•2n-1,④
③-④得
-Sn=1+2+22+…+2n-2-n•2n-1
=
-n•2n-1
=(1-n)•2n-1-1,
∴Sn=(n-1)•2n-1+1.
即2a1q=a1+a1q2-1,
∵a1=1,∴2q=q2,
∵q≠0,∴q=2,an=2n-1.
又b1+
| b2 |
| 2 |
| b3 |
| 3 |
| bn |
| n |
当n≥2时,b1+
| b2 |
| 2 |
| b3 |
| 3 |
| bn-1 |
| n-1 |
①-②,得
| bn |
| n |
∴bn=n•2n-2,n≥2.
∴bn=
|
(2)由(1)得Sn=1+2×20+3×21+4×22+…+n•2n-2,③
2Sn=2+2×21+3×22+…+(n-1)•2n-2+n•2n-1,④
③-④得
-Sn=1+2+22+…+2n-2-n•2n-1
=
| 1-2n-1 |
| 1-2 |
=(1-n)•2n-1-1,
∴Sn=(n-1)•2n-1+1.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
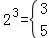 ,
,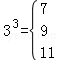 ,
,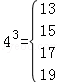 ,….仿此,若m3的“分裂数”中有一个是2015,则m= _________ .
,….仿此,若m3的“分裂数”中有一个是2015,则m= _________ .