题目内容
在等比数列{an}中,an>0,(n∈N*),公比q>1,a1a3+2a2a4+a3a5=100,且4是a2与a4的等比中项,
(1)求数列{an}的通项公式;
(2)设bn=an2+log2an,求数列{bn}的前n项和Sn.
(1)求数列{an}的通项公式;
(2)设bn=an2+log2an,求数列{bn}的前n项和Sn.
(1)设等比数列{an}的公比为q,则an=a1qn-1,
由已知得a1a3+2a2a4+a3a5=(a2+a4)2=100,
∵an>0,(n∈N*),
∴a2+a4=10,
∵4是a2与a4的等比中项,
∴a2a4=42=16,
∴a2,a4是方程x2-10x+16=0的两个根,
∵q>1,∴a2=2,a4=8,
∴
,解得a1=1,q=2,
∴an=2n-1.
(2)∵an=2n-1,
∴bn=an2+log2an=4n-1+(n-1),
∴数列{bn}的前n项和
Sn=(1+4+42+…+4n-1)+(1+2+3+…+n-1)
=
+
.
由已知得a1a3+2a2a4+a3a5=(a2+a4)2=100,
∵an>0,(n∈N*),
∴a2+a4=10,
∵4是a2与a4的等比中项,
∴a2a4=42=16,
∴a2,a4是方程x2-10x+16=0的两个根,
∵q>1,∴a2=2,a4=8,
∴
|
∴an=2n-1.
(2)∵an=2n-1,
∴bn=an2+log2an=4n-1+(n-1),
∴数列{bn}的前n项和
Sn=(1+4+42+…+4n-1)+(1+2+3+…+n-1)
=
| 4n-1 |
| 3 |
| n(n-1) |
| 2 |

练习册系列答案
相关题目
 ,数列
,数列 的前
的前 项和为
项和为 ,点
,点 均在函数
均在函数 的图象上.
的图象上. ;
;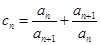 ,证明:
,证明: .
.