题目内容
抛物线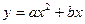 在第一象限内与直线
在第一象限内与直线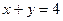 相切。此抛物线与x轴所围成的
相切。此抛物线与x轴所围成的 图形的面积记为S。求使S达到最大值的a,b值,并求
图形的面积记为S。求使S达到最大值的a,b值,并求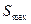 。
。
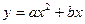 在第一象限内与直线
在第一象限内与直线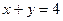 相切。此抛物线与x轴所围成的
相切。此抛物线与x轴所围成的 图形的面积记为S。求使S达到最大值的a,b值,并求
图形的面积记为S。求使S达到最大值的a,b值,并求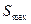 。
。解:依题设可知抛物线为凸形,它与x轴的交点的横坐标分别为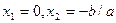 ,所以
,所以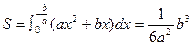 (1)
(1)
又直线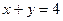 与抛物线
与抛物线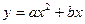 相切,即它们有唯一的公共点
相切,即它们有唯一的公共点
由方程组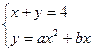
得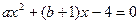 ,其判别式必须为0,即
,其判别式必须为0,即
于是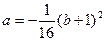 ,代入(1)式得:
,代入(1)式得: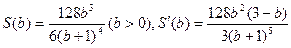
令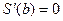 ;在
;在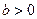 时得唯一零点
时得唯一零点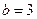 ,且当
,且当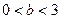 时,
时, ;当
;当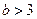 时,
时,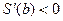 。故在
。故在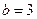 时,
时,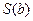 取得极大值,也是最大值,即
取得极大值,也是最大值,即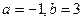 时,S取得最大值,且
时,S取得最大值,且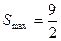
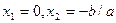 ,所以
,所以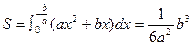 (1)
(1)又直线
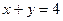 与抛物线
与抛物线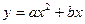 相切,即它们有唯一的公共点
相切,即它们有唯一的公共点由方程组
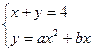
得
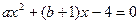 ,其判别式必须为0,即
,其判别式必须为0,即
于是
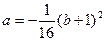 ,代入(1)式得:
,代入(1)式得: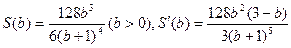
令
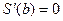 ;在
;在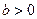 时得唯一零点
时得唯一零点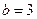 ,且当
,且当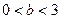 时,
时, ;当
;当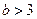 时,
时,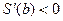 。故在
。故在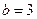 时,
时,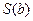 取得极大值,也是最大值,即
取得极大值,也是最大值,即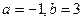 时,S取得最大值,且
时,S取得最大值,且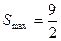
略

练习册系列答案
相关题目
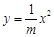 的焦点坐标为( ) .
的焦点坐标为( ) . 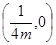
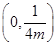
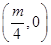
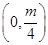
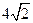 m,在水面以上部分高为4m的船船身应至少降低多少米才能安全通过?
m,在水面以上部分高为4m的船船身应至少降低多少米才能安全通过?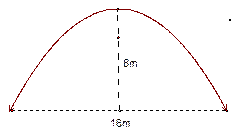
 上异于坐标原点O的两不同动点A、B满足
上异于坐标原点O的两不同动点A、B满足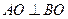 (如图所示).
(如图所示).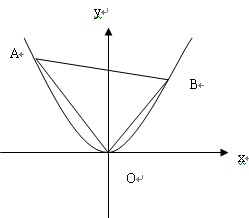
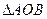 得重心G(即三角形三条中线的交点)的轨迹方程;
得重心G(即三角形三条中线的交点)的轨迹方程;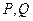 是抛物线
是抛物线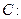
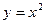 上两动点,直线
上两动点,直线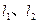 分别是抛物线
分别是抛物线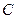 在点
在点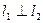 ,
,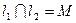 .
. 1)求点
1)求点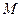 的纵坐标;
的纵坐标;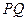 是否经过一定点
是否经过一定点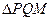 的面积的最小值
的面积的最小值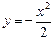 与过点
与过点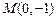 的直线
的直线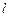 相交于
相交于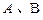 两点,
两点,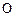 为原点.若
为原点.若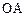 和
和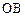 的斜率之和为1,(1)求直线
的斜率之和为1,(1)求直线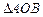 的面积.
的面积.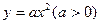 的焦点F作一直线交抛物线于P、Q两点,若线段PF与FQ的长分别为p、q,则
的焦点F作一直线交抛物线于P、Q两点,若线段PF与FQ的长分别为p、q,则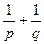 等于 ( )
等于 ( ) 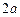
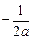
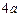
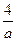
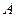 、
、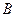 是抛物线
是抛物线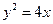 上的两个点,
上的两个点,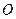 是坐标原点,若
是坐标原点,若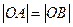 ,且
,且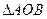 的垂心恰是抛物线的焦点,则
的垂心恰是抛物线的焦点,则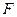 为抛物线
为抛物线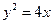 的焦点,
的焦点,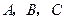 为该抛物线上三点,若
为该抛物线上三点,若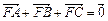 ,则
,则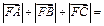 ( )
( )