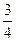题目内容
(13分)
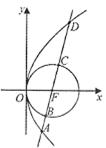
在平面直角坐标系xOy中,抛物线 上异于坐标原点O的两不同动点A、B满足
上异于坐标原点O的两不同动点A、B满足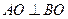 (如图所示).
(如图所示).
(Ⅰ)求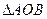 得重心G(即三角形三条中线的交点)的轨迹方程;
得重心G(即三角形三条中线的交点)的轨迹方程;
(Ⅱ)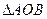 的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
在平面直角坐标系xOy中,抛物线
 上异于坐标原点O的两不同动点A、B满足
上异于坐标原点O的两不同动点A、B满足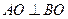 (如图所示).
(如图所示).
(Ⅰ)求
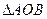 得重心G(即三角形三条中线的交点)的轨迹方程;
得重心G(即三角形三条中线的交点)的轨迹方程;(Ⅱ)
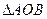 的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.解:(I)设△AOB的重心为G(x,y),A(x1,y1),B(x2,y2),则
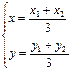 (1)…1分
(1)…1分∵OA⊥OB ∴
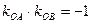 ,即
,即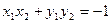 ,(2)…………3分
,(2)…………3分又点A,B在抛物线上,有
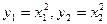 ,代入(2)化简得
,代入(2)化简得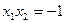 …4分
…4分∴
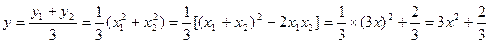
所以重心为G的轨迹方程为

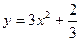 ……………………………………6分
……………………………………6分(II)
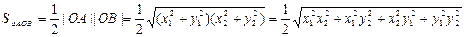
由(I)得
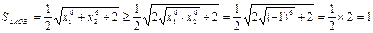 ……11分
……11分当且仅当
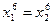 即
即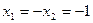 时,等号成立。………………………12分
时,等号成立。………………………12分所以△AOB的面积存在最小值,存在时求最小值1; …………………13分

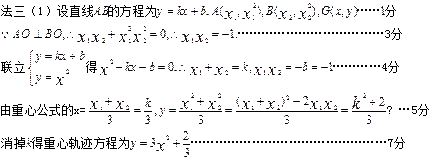
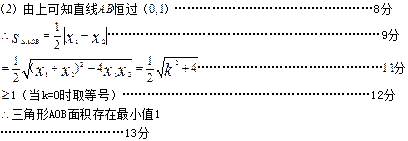
略

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
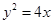 的焦点F作直线
的焦点F作直线 交抛物线于A,B两点,若
交抛物线于A,B两点,若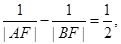 则直线
则直线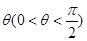 等于( )
等于( )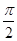
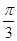
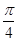
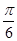
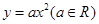 的准线方程为
的准线方程为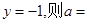 。
。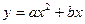 在第一象限内与直线
在第一象限内与直线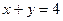 相切。此抛物线与x轴所围成的
相切。此抛物线与x轴所围成的 图形的面积记为S。求使S达到最大值的a,b值,并求
图形的面积记为S。求使S达到最大值的a,b值,并求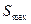 。
。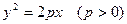 上有一点
上有一点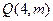 到焦点
到焦点 的距离为5,
的距离为5,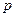 及
及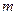 的值。
的值。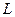 交抛物线于A,B两点,若
交抛物线于A,B两点,若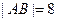 ,求直线
,求直线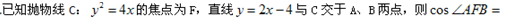

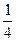 为准线的抛物线的标准方程为 ( )
为准线的抛物线的标准方程为 ( )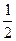 x
x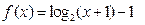 的零点是抛物线
的零点是抛物线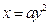 焦点的横坐标,则
焦点的横坐标,则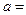
 .
.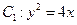 和圆
和圆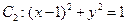 ,直线
,直线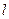 经过C1的焦点F,依次交C1,C2于A,B,C,D四点,则
经过C1的焦点F,依次交C1,C2于A,B,C,D四点,则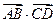 的值为( )
的值为( )