题目内容
5.下列各函数中,最小值为4的是( )| A. | y=x+$\frac{4}{x}$ | B. | y=sinx+$\frac{4}{sinx}$,x∈(0,$\frac{π}{2}$) | ||
| C. | y=$\frac{{x}^{2}+2}{\sqrt{{x}^{2}+1}}$ | D. | y=$\sqrt{x}$+$\frac{9}{\sqrt{x}}$-2 |
分析 利用函数的性质以及基本不等式求解即可.
解答 解:y=x+$\frac{4}{x}$中,x≠0,所以最小值不为4.
y=sinx+$\frac{4}{sinx}$=sinx+$\frac{1}{sinx}+\frac{3}{sinx}$≥5,x∈(0,$\frac{π}{2}$),最小值不是4.
y=$\frac{{x}^{2}+2}{\sqrt{{x}^{2}+1}}$≥2,最小值不是4;
y=$\sqrt{x}$+$\frac{9}{\sqrt{x}}$-2≥$2\sqrt{\sqrt{x}×\frac{9}{\sqrt{x}}}$-2=4,当且仅当x=9时取等号.满足题意.
故选:D.
点评 本题考查函数的最值以及基本不等式的应用,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.县政府组织500人参加卫生城市创建“义工”活动,按年龄分组所得频率分布直方图如下图,完成下列问题:
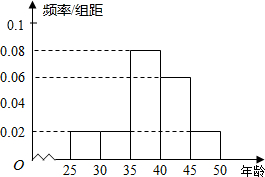
(1)如表是年龄的频数分布表,求出表中正整数a、b的值;
(2)现在要从年龄较小的第1、2、3组中用分层抽样的方法抽取6人,则年龄在第1、2、3组的各抽取多少人?
(3)在第(2)问的前提下,从这6人中随机抽取2人参加社区活动,求至少有1人年龄在第3组的概率.

| 组别 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50) |
| 人数 | 50 | 50 | a | 150 | b |
(2)现在要从年龄较小的第1、2、3组中用分层抽样的方法抽取6人,则年龄在第1、2、3组的各抽取多少人?
(3)在第(2)问的前提下,从这6人中随机抽取2人参加社区活动,求至少有1人年龄在第3组的概率.
20.在△ABC中,a,b,c分别为角A,B,C所对的边,若a2<b2-c2,则△ABC的形状为( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 不能确定 |
14.已知等比数列{an}的前n项和为Sn,则下列一定成立的是( )
| A. | 若a3>0,则a2015<0 | B. | 若a4>0,则a2015<0 | ||
| C. | 若a3>0,则a2015>0 | D. | 若a4>0,则a2015>0 |