题目内容
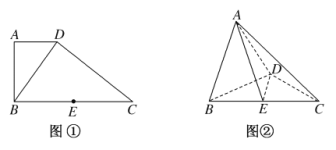
【题目】如图①,在直角梯形中![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 边的中点,将
边的中点,将![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,连接
,连接![]() ,
,![]() ,
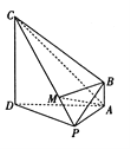
,![]() ,得到如图②所示的几何体.
,得到如图②所示的几何体.
(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() ,二面角
,二面角![]() 的平面角的正切值为
的平面角的正切值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)要证![]() 平面
平面![]() ,只需证明
,只需证明![]() 和
和![]() ,即可求得答案;
,即可求得答案;
(2)根据已知求得![]() ,
,![]() ,
,![]() ,建立空间直角坐标系
,建立空间直角坐标系![]() ,求得平面
,求得平面![]() 的法向量
的法向量![]() 和平面
和平面![]() 的法向量
的法向量![]() ,即可求得答案.
,即可求得答案.
(1)![]() 平面
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]()
![]()
![]() 平面
平面![]()
![]()
![]() 平面
平面![]() ,
,
![]()
![]()
又![]() 折叠前后均有
折叠前后均有![]() ,
,![]()
![]()
![]() 平面
平面![]()
(2)![]() (1)知
(1)知![]() 平面
平面![]() ,
,
![]() 二面角
二面角![]() 的平面角为
的平面角为![]()
又![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]()
![]()
依题意![]()
![]()
![]() ,所以
,所以![]() ,
,
设![]()
则![]()
依题意![]() ,
,
![]()
![]()
即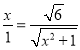
解得![]() ,
,
故![]() ,
,![]() ,
,![]()
如图所示,建立空间直角坐标系![]()
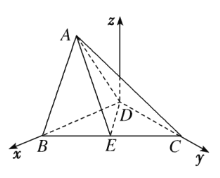
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]()
![]() ,
,![]()
由(1)知平面![]() 的一个法向量
的一个法向量![]()
设平面![]() 的法向量为
的法向量为![]()
由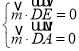 ,得
,得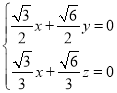
令![]() ,得
,得![]() ,
,![]() ,
,
![]()
![]() 为平面
为平面![]() 的一个法向量
的一个法向量
![]()
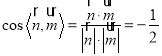
由图可知二面角![]() 的平面角为锐角
的平面角为锐角
![]() 二面角
二面角![]() 的余弦值为
的余弦值为![]()

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
【题目】从某大学中随机选取7名女大学生,其身高x(单位:cm)和体重y(单位:kg)数据如下表:
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
身高x | 163 | 164 | 165 | 166 | 167 | 168 | 169 |
体重y | 52 | 52 | 53 | 55 | 54 | 56 | 56 |
(1)求y关于x的回归方程;
(2)利用(1)中的回归方程,分析这7名女大学生的身高和体重的变化,并预报一名身高为172cm的女大学生的体重.