题目内容
【题目】已知
为坐标原点，椭圆
：
上顶点为
，右顶点为
，离心率
，圆：
与直线
相切.
（1）求椭圆的标准方程；
（2）若
，
，
为椭圆上的三个动点，直线
，
，
的斜率分别为
.
（i）若的中点为
，求直线的方程；
（ii）若
，证明：直线过定点.
【答案】（1）
；（2）（i）
；（ii）证明见解析.
【解析】
（1）由离心率和直线AB与圆相切分别得到a，b的关系式，求解得椭圆的方程；
（2）（i）由点差法求出直线EF的斜率，然后写出方程；
（ⅱ）由直线DE、DF与椭圆的相交关系，分别求出E、F两点的横坐标，再利用
，求得
，另设直线
的方程为
，代入椭圆方程，利用韦达定理表示
，求得
，故得结论直线EF过定点
．
解：（1）由题意，直线
的方程为：
，即为
，
因为圆
与直线相切，所以
，
①
设椭圆的半焦距为
，因为
，
，
所以
②
由①②得：
，
，所以椭圆
的标准方程为：.
（2）设
，
，
，
（i）由题知：
，
，
两式做差得：
，，
整理得：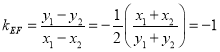
，
所以此时直线的方程为：；
（ii）设直线
：
，设直线
：
，
将
代入，
得：
，
所以
，
，
因此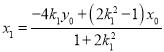
.
又因为，且同理可得：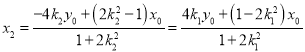
，
可得，
设直线的方程为：，将代入，
得：
，
得
，所以，
所以直线过定点
.
能考试期末冲刺卷系列答案
【题目】某产品的广告支出
（单位：万元）与销售收入
（单位：万元）之间有下表所对应的数据：
广告支出 | 1 | 2 | 3 | 4 |
销售收入 | 12 | 28 | 42 | 56 |
（1）画出表中数据的散点图；
（2）求出对的线性回归方程；
（3）若广告费为9万元，则销售收入约为多少万元？
【题目】某重点中学高三的一名学生在高考前对他在高三近一年中的所有数学考试(含模拟考试、月考、平时训练等各种类型的试卷)分数进行统计，以此来估计自己在高考中的大致分数.为此，随机抽取了若干份试卷作为样本，根据此样本数据作出如下频率分布统计表和频率分布直方图.
分组 | 频数 | 频率 |
| 20 | 0.25 |
| 50 |
|
|
|
|
| 4 | 0.05 |
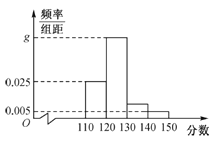
（1）求表中
的值和频率分布直方图中
的值；
（2）若同组中的每个数据用该组区间的中点值代替，试根据频率分布直方图求该学生高三年级数学考试分数的中位数和平均数，并对该学生自己在高考中的数学成绩进行预测.