题目内容
【题目】已知正
所在平面垂直平面
，且边
在平面内，过
、
分别作两个平面
、
（与正所在平面不重合），则以下结论错误的是( )
A.存在平面与平面，使得它们的交线
和直线所成角为
B.直线与平面所成的角不大于
C.平面与平面所成锐二面角不小于
D.平面与平面所成锐二面角不小于
【答案】D
【解析】
结合空间中的直线和平面的关系，平面与平面的关系，以及图形进行判定.
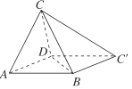
如图1，设平面
与平面
相交于
，且点
在平面
内.
对于选项A：设
的中点为
，则当
为等边三角形时，易得
，所以
平面
，所以
，故正确；
对于选项B：由最小角定理得直线与平面所成角小于等于
，故正确；
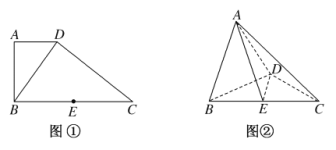
对于选项C：过点作
，垂足为
，如图2所示，易得
，则
，则平面平面与平面所成锐二面角不小于
，故正确；
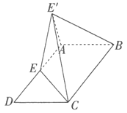
对于选项D：过点
作
交于点
，过点作
交
于点
,
如图3所示，则
为平面与平面所成锐二面角（或补角），因为
为定值，点在直线上运动，当
无穷大时，
，此时平面与平面所成锐二面角不小于，故错误.
故选：D.
练习册系列答案
阅读快车系列答案
相关题目
